潮汐静力学理论(卷名：大气科学 海洋科学 水文科学)
static theory of tides
自从I.牛顿用引潮力解释潮汐运动之后，潮汐动力的基本问题已经清晰，但用牛顿的理论直接研究海洋中的潮汐问题时，遇到非常复杂的数学困难。为此，必须将海洋所占据的空间区域，理想化为它具有简单的几何形状。1740年，D.伯努利从静力学平衡的角度出发，假设地球表面都被海洋所覆盖，而且海面在任何时刻都能够保持与重力和引潮力的合力处处垂直。这种理想化了的海洋潮汐，称为平衡潮。伯努利的这种学说，称为平衡潮学说。在此学说的基础上建立起来的一种潮汐理论，为潮汐静力学理论。这是继牛顿之后第一个提出的潮汐理论。
由此理论得到，地球表面由月球引潮力所产生的太阳平衡潮的潮高
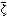为
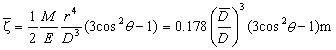式中γ为地球半径的平均值，θ为月球的天顶距，M 为月球的质量，E 为地球的质量，D为月-地距离，哹 为月-地平均距离，m 为长度单位“米”。由太阳引潮力所产生的太阳平衡潮的潮高，也有类似的表达式。如果在公式中取D =哹，且当θ=0°或180°时，
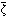=0.356米，而当θ=90°或270°时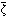，=-0.178米，这表明平衡潮面在对着月球和背着月球的地点形成高潮，而在矢径与地球和月球的中心连线垂直的地点，形成低潮。对固定地点来说，由于地球自转和月球绕地球公转，月中天时刻每天约推迟50分钟，因此潮汐在一个太阴日（平均约24时50分）内通常有两次高潮和两次低潮，而且高潮和低潮发生的时刻，平均每天都推迟50分钟。每逢朔日或望日，月球和太阳在天球上的经度差不多相等或相差180°，此时太阴潮和太阳潮叠加的结果，使当地的潮汐涨落在每半个月当中最大，称为大潮。若月-地距离和日-地距离都取平均值，则大潮时潮差的理论值可达0.78米。每逢上弦和下弦，太阳和月球在天球上的经度大致相差90°，此时因太阴潮和太阳潮互相削弱的效果最大，就使当地的潮汐涨落在每半个月当中最小，称为小潮。如果月-地距离和日-地距离都取平均值，则小潮时潮差的理论值可低达0.29米。实际上，对太阴潮和太阳潮来说，哹/D 的极大值分别为1.071和1.017，其立方分别为1.23和1.05，故太阴平衡潮的潮差最大可达0.657米，太阳平衡潮的潮差最大可达0.258米，两者之和应为0.915米，这是平衡潮的潮差能够达到的最大值。
大洋里许多岛屿的大潮差大多接近1米。例如:中国台湾东岸的火烧岛附近的大潮差约为 1米；夏威夷群岛火奴鲁鲁一带的最大潮差约为0.9米。 这都接近于从平衡潮理论算出的数值。但在陆架海区，由于潮波能量的集中，因而潮差往往比上述数字大得多。例如：中国杭州湾的澉浦，曾测得最大潮差为8.93米；北美洲芬迪湾的潮差在世界上最大，大约比杭州湾大一倍。
为了说明潮汐的周期和振幅的变化，在前面公式中引入月球天顶距θ与月球赤纬δ、当地纬度φ和月球时角A 的关系，则前面的太阴平衡潮公式可化为
对于太阳平衡潮来说，也有类似的表达式。此公式表明，太阴平衡潮具有 3种基本周期：半日周期、全日周期和长周期。就时角A而言，对地球上任何地点来说，由于月球和太阳都约有360°的时角变化，2A在一日之间有720°的变化，故第一项为半日周期项，它的振幅与cos2δ 成正比，而月球的δ 变化范围为0°～±28.6°，故cos2δ变化于0.77～1.00之间，因此对一定地点来说，太阴（太阳）半日潮的高(低)潮的时间主要决定于时角，但月-地（日-地）距离和月球 (太阳)赤纬对潮差也有一定的影响。式中第二项的时角为全日周期项，但是对于月球来说，sin2δ大约具有周期为半个月的变化，而对于太阳则具有周期为半年的变化。在赤纬为0°时，全日周期项为零；当赤纬不为零时，除赤道外，在地球上其他各点，半日潮和全日潮同时存在，叠加的结果，就出现日潮不等的现象。随着赤纬的增大，日潮不等的现象更加显著，在赤纬达极值时最为突出。公式的第三项不包括时角，仅由赤纬决定。对于月球，其周期约为半个月；对于太阳，则为半年。这都属于潮汐变化中的长周期部分。平衡潮学说虽能定性地说明潮汐的周期变化和不等现象，但实际的海洋潮汐是一种复杂的波动现象(潮波)，属于流体动力学范畴，其运动规律不是静力学理论所能阐明的。