矩阵(卷名:数学)
matrix
数学中最重要的基本概念之一,是代数学的一个主要研究对象,也是数学研究及应用的一个重要工具。由mn个数排成的m行n列的矩形表
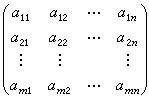 称为m×n矩阵,记作A或
称为m×n矩阵,记作A或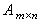 ,也可记作(αij)或
,也可记作(αij)或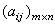 。数
。数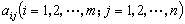 称为矩阵的第i行第j列的元素。当矩阵的元素都是某一数域F中的数时,就称它为数域F上的矩阵,简称F上的矩阵。当m=n时,矩阵A称为n阶矩阵或n阶方阵,此时α11,α22,…,αnn称为n阶矩阵的对角线元素,当所有的非对角线元素αij(i≠j)均为零时,A就称为n阶对角矩阵,简称对角矩阵。当对角线下面(或上面)的所有元素均为0时,A就称为上(或下)三角矩阵。
称为矩阵的第i行第j列的元素。当矩阵的元素都是某一数域F中的数时,就称它为数域F上的矩阵,简称F上的矩阵。当m=n时,矩阵A称为n阶矩阵或n阶方阵,此时α11,α22,…,αnn称为n阶矩阵的对角线元素,当所有的非对角线元素αij(i≠j)均为零时,A就称为n阶对角矩阵,简称对角矩阵。当对角线下面(或上面)的所有元素均为0时,A就称为上(或下)三角矩阵。在m×n矩阵A中取k个行和k个列,k≤m,n;由这些行与列相交处的元素按原来的位置构成的k阶行列式,称为矩阵A的k阶子式。一个n阶矩阵A只有一个n阶子式,它称为矩阵A的行列式,记作│A│或detA。
矩阵的运算 两个矩阵只有在其行数与列数均分别相同,而且所有相应位置的元素均相等时,才能称为相等。只有在两个矩阵的行数与列数均分别相同时,才能进行加法。矩阵
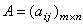 与
与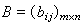 相加而得和
相加而得和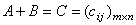 ,其中
,其中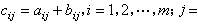
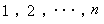 。 数乘矩阵是指数域F中任何数 α 均可去乘F上任意矩阵
。 数乘矩阵是指数域F中任何数 α 均可去乘F上任意矩阵  而得积
而得积 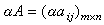 ,即αA仍为m×n矩阵,其第i行第j列的元素为ααij,i=1,2,…,m ;j=1,2,…,n。只有一个矩阵的列数等于另一个矩阵的行数时,这两个矩阵才能进行乘法:一个m×n矩阵A=(αij)去乘一个n×p 矩阵B=(bij)而得积AB是一个m ×p 矩阵D =(dij),其中
,即αA仍为m×n矩阵,其第i行第j列的元素为ααij,i=1,2,…,m ;j=1,2,…,n。只有一个矩阵的列数等于另一个矩阵的行数时,这两个矩阵才能进行乘法:一个m×n矩阵A=(αij)去乘一个n×p 矩阵B=(bij)而得积AB是一个m ×p 矩阵D =(dij),其中 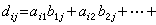
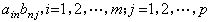 ,即AB的行数与A的行数相同,而其列数与B 的列数相同。此种乘法规则也适用于分块矩阵(即将元素划分成若干小矩阵块的矩阵)。分块时A的列的分法应与B的行的分法一致。矩阵运算有以下性质:
,即AB的行数与A的行数相同,而其列数与B 的列数相同。此种乘法规则也适用于分块矩阵(即将元素划分成若干小矩阵块的矩阵)。分块时A的列的分法应与B的行的分法一致。矩阵运算有以下性质:A+B=B+A;A+(B+C)=(A+B)+C;α(A+B)=αA+αB;(α+β)A=αA+βA;α(βA)=(αβ)A;α(AB)=(αA)B=A(αB);A(BC)=(AB)C;(A+B)C=AC+BC;A(B+C)=AB+AC,这里A、B、C表示矩阵,α表示数域F中的数。
当一个m×n矩阵的全部元素均为0时,就称为零矩阵,记作Om×n。对于任意一个m×n矩阵A,恒有A+Om×n=A;且恒有惟一的一个m×n矩阵B=(-1)A,使A+B=Om×n,此B称为A的负矩阵,简记为-A。易知-A的负矩阵就是A,即-(-A)=A。
数域F上的所有 m×n矩阵按上述矩阵加法和数乘矩阵运算,构成F上的一个m n维向量空间;F上的所有n阶矩阵按矩阵的加法和乘法构成一个环,称为F上的n阶全阵环。F上的n阶全阵环视为F上的n2维向量空间,就构成F上的n阶全阵代数。
单位矩阵与逆矩阵 对角线元素都是 1的 n阶对角矩阵,称为n阶单位矩阵,简记为In。对于任意矩阵Am×n与Bn×p, 恒有
 ,对于任意n阶矩阵A,恒有AIn=InA=A。若对于一个n阶矩阵A,有一个n阶矩阵B存在,使AB=BA=In,则B称为A的逆矩阵,记作A-1。易知B即A-1是由A惟一确定的。当A有逆矩阵A-1时,A-1也有逆矩阵且就是A,即(A-1)-1=A。有逆矩阵的n阶矩阵,称为非奇异矩阵;没有逆矩阵的n阶矩阵,称为奇异矩阵。当A和B都是n阶非奇异矩阵时,则AB也是非奇异矩阵,且(AB)-1=B-1A-1。这个等式用数学归纳法可推广到任意有限多个n阶非奇异矩阵的情形。
,对于任意n阶矩阵A,恒有AIn=InA=A。若对于一个n阶矩阵A,有一个n阶矩阵B存在,使AB=BA=In,则B称为A的逆矩阵,记作A-1。易知B即A-1是由A惟一确定的。当A有逆矩阵A-1时,A-1也有逆矩阵且就是A,即(A-1)-1=A。有逆矩阵的n阶矩阵,称为非奇异矩阵;没有逆矩阵的n阶矩阵,称为奇异矩阵。当A和B都是n阶非奇异矩阵时,则AB也是非奇异矩阵,且(AB)-1=B-1A-1。这个等式用数学归纳法可推广到任意有限多个n阶非奇异矩阵的情形。转置矩阵 一个 m×n矩阵A的行与列的元素互换而得到的n×m矩阵,称为A的转置矩阵,记为A′或AT。若A是一个n阶方阵,且A′=A,则A称为对称矩阵。关于矩阵的转置,有如下基本运算规律:(A′)′=A;(A+B)′=A′+B′;(αA)′=α(A′);(AB)′=B′A′。
n阶矩阵A =(αij)的元素αij在│A│中的代数余子式Aij(i,j=1,2,…,n)仍是数域F中的数,于是可作成如下的一个n阶矩阵
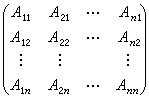 ,并记为Ã0。矩阵Ã0,称为A的伴随矩阵。由行列式的性质可知,A为非奇异矩阵,必要而且只要 │A│≠0,此时有
,并记为Ã0。矩阵Ã0,称为A的伴随矩阵。由行列式的性质可知,A为非奇异矩阵,必要而且只要 │A│≠0,此时有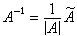 。
。秩数与迹数 一个m×n矩阵A的每行可看成一个n元向量(即n元数列),称为A的行向量。m×n矩阵A就有m个行向量,这m个行向量中的线性无关极大组所含向量的个数,即行向量的秩数,称为A的行秩数。可类似定义A的列秩数。任意矩阵A的行秩数恒等于其列秩数,因此可简称为A的秩数。A的秩数等于A的非零子式的最大阶数。一个n阶矩阵A的对角线元素的和,称为A的迹数。对任意n阶矩阵A与B,(A+B)的迹数=A的迹数+B的迹数;(kA)的迹数=k(A的迹数),这里k为某个数。
环上的矩阵 若用一个环R 去代替数域F,则可定义R上的矩阵及其运算,而且上述有关数域F上的内容,绝大部分都可以推广到R上,尤其当R是一个有单位元素1的交换环,甚至是一个域时,则上述的全部内容可以推广到R上。R是一个域或复数域F上的多项式环F[λ]的情形最为有用。
若A=(αij)是复数域F上的一个n阶矩阵,I是n阶单位矩阵,则A、I以及λI-A都可视为多项式环F[λ]上的n阶矩阵
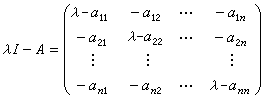 称为A 的特征矩阵。其行列式|λI-A|是F[λ]中的一个首项系数为1的 n 次多项式
称为A 的特征矩阵。其行列式|λI-A|是F[λ]中的一个首项系数为1的 n 次多项式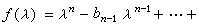 (-1)nb0,其中bn-1恰为A的迹数,b0恰为|A|,ƒ(λ)=|λI-A|称为A的特征多项式,其根称为A的特征值或特征根。λ0为A的一个特征值,必要而且只要有F上非零的n元列向量ξ即n行1列的矩阵,使λ0ξ=Aξ。此ξ称为A的属于λ0的一个特征向量。A的属于不同特征值的特征向量,恒在F上线性无关。
(-1)nb0,其中bn-1恰为A的迹数,b0恰为|A|,ƒ(λ)=|λI-A|称为A的特征多项式,其根称为A的特征值或特征根。λ0为A的一个特征值,必要而且只要有F上非零的n元列向量ξ即n行1列的矩阵,使λ0ξ=Aξ。此ξ称为A的属于λ0的一个特征向量。A的属于不同特征值的特征向量,恒在F上线性无关。对于F[λ]中任意一个m次多项式
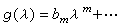
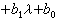 ,可以用F上任意一个n阶矩阵A去代替λ而引出一个n阶矩阵
,可以用F上任意一个n阶矩阵A去代替λ而引出一个n阶矩阵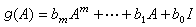 ,其中I为n阶单位矩阵。所谓凯莱-哈密顿定理,即如果ƒ(λ)是F上n阶矩阵A的特征多项式时,那么恒有ƒ(A)=On,其中On为n阶零矩阵。由此可知,对于F上任意n阶矩阵A,必存在唯一的首项系数为1的多项式φ(λ)使φ(A)=On。对于任意的多项式 g(λ),g(A)=On 必要而且只要φ(λ)|g(λ)(即φ(λ)能整除g(λ))。此φ(λ)就称为A的最小多项式。
,其中I为n阶单位矩阵。所谓凯莱-哈密顿定理,即如果ƒ(λ)是F上n阶矩阵A的特征多项式时,那么恒有ƒ(A)=On,其中On为n阶零矩阵。由此可知,对于F上任意n阶矩阵A,必存在唯一的首项系数为1的多项式φ(λ)使φ(A)=On。对于任意的多项式 g(λ),g(A)=On 必要而且只要φ(λ)|g(λ)(即φ(λ)能整除g(λ))。此φ(λ)就称为A的最小多项式。矩阵的等价 对矩阵A的行与列或仅对行或仅对列施以若干次初等变换而得到矩阵B,称为A等价于B,记为A≌B。矩阵之间的这个关系具有反身性、对称性和传递性,所以它是一种等价关系。矩阵的等价是在讨论一个向量空间到另一个向量空间的线性变换的各种矩阵表示问题中产生的。所谓矩阵的初等变换,是指以下的任何一种变换:①用F中任意的一个不为零的元素α去乘矩阵的第i行(列);②把矩阵的第i行(列)的b倍加于第j行(列),其中b为F中任意元素;③互换矩阵的第i与第j行(列),并分别称为第一、第二、第三种初等变换。
对F上的单位矩阵I进行一次初等变换后所得出的矩阵,称为初等矩阵。一种初等变换对应于一种初等矩阵。对矩阵A的行施以某种初等变换的结果,恰等于用相应的初等矩阵去左乘A;对A的列施以某种初等变换的结果,恰等于用相应的初等矩阵去右乘A。初等矩阵恒为可逆的,且其逆矩阵仍是同一种初等矩阵,因此初等矩阵的积恒为非奇异矩阵。由此可知,等价矩阵的秩数相同,或者说初等变换不改变矩阵的秩数。于是,经若干次初等变换后,必可将每个秩数为r的矩阵的左上角化为r阶单位矩阵,而其他位置都化为0。n阶非奇异矩阵恒等价于n阶单位矩阵,恒可表为若干个初等矩阵之积。因此,A≌B必要而且只要有非奇异矩阵P、Q使PAQ=B。
多项式环F[λ]上的矩阵
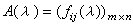 ,简称为λ矩阵。在F[λ]上也可定义行列式。A(λ)的秩数定义为A(λ)的最大非零子式的阶数。对λ矩阵也可进行初等变换,在第一种初等变换中只能使用F中非零的α,而不能用F[λ]中非零的ƒ(λ);第二种初等变换中则可用F[λ]中任意的g(λ)去代替b。也可以定义可逆性,对于λ矩阵P(λ)若有λ矩阵K(λ)使P(λ)K(λ)=K(λ)P(λ)=I,则称λ矩阵P(λ)是可逆的,λ矩阵K(λ)则称为P(λ)的逆矩阵。也可以定义λ矩阵的等价。秩数为r的λ矩阵A(λ)必等价于所谓A(λ)的法式即λ矩阵:
,简称为λ矩阵。在F[λ]上也可定义行列式。A(λ)的秩数定义为A(λ)的最大非零子式的阶数。对λ矩阵也可进行初等变换,在第一种初等变换中只能使用F中非零的α,而不能用F[λ]中非零的ƒ(λ);第二种初等变换中则可用F[λ]中任意的g(λ)去代替b。也可以定义可逆性,对于λ矩阵P(λ)若有λ矩阵K(λ)使P(λ)K(λ)=K(λ)P(λ)=I,则称λ矩阵P(λ)是可逆的,λ矩阵K(λ)则称为P(λ)的逆矩阵。也可以定义λ矩阵的等价。秩数为r的λ矩阵A(λ)必等价于所谓A(λ)的法式即λ矩阵: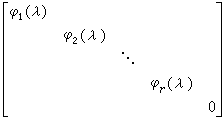 ,这里的诸φi(λ)均由A(λ)惟一确定,且φ1(λ)|φ2(λ)|…|φr(λ),首项系数均为1。
,这里的诸φi(λ)均由A(λ)惟一确定,且φ1(λ)|φ2(λ)|…|φr(λ),首项系数均为1。由此可知,一个n阶λ矩阵P(λ)是可逆的,必要而且只要P(λ)为若干个与λ矩阵的初等变换相应的初等矩阵的积;必要而且只要其行列式为F 中的非零元素。两个λ矩阵A(λ)m×n,B(λ)m×n是等价的,必要而且只要有可逆λ矩阵P(λ)、Q(λ)使P(λ)A(λ)Q(λ)=B(λ)。A(λ)的法式中的诸多项式φi(λ),都称为A(λ)的不变因子,且可作如下分解:
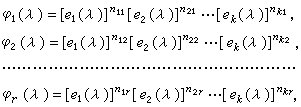 式中诸ej(λ)是F[λ]中首项系数为1的互不相同的既约多项式;nij为非负整数,且最后一行中的n1r,n2r,…,nkr均非零,并有
式中诸ej(λ)是F[λ]中首项系数为1的互不相同的既约多项式;nij为非负整数,且最后一行中的n1r,n2r,…,nkr均非零,并有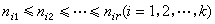 。这些因子
。这些因子 ,除去指数nij=0者,都称为A(λ)的初等因子。
,除去指数nij=0者,都称为A(λ)的初等因子。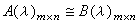 必要而且只要它们的法式相同;必要而且只要它们的全部不变因子一致;必要而且只要它们的秩数与全部初等因子一致。
必要而且只要它们的法式相同;必要而且只要它们的全部不变因子一致;必要而且只要它们的秩数与全部初等因子一致。矩阵的相似 对于域F上两个n阶矩阵A、B,若有非奇异矩阵P,使P-1AP=B,则称为A相似于B,记为A~B。矩阵之间的这个关系,具有反身性、对称性和传递性,所以它是一种等价关系。矩阵的相似是在讨论一个向量空间到自身之间的线性变换的各种矩阵表示问题中产生的。域F上两个n阶矩阵A与B相似,必要而且只要特征矩阵(λI-A)与(λI-B)在F[λ]上等价。λI-A的不变因子与初等因子,分别称为A的不变因子与初等因子。特征矩阵λI-A的秩数,即A的阶数n。因此,在F上的两个n阶矩阵A与B相似,必要而且只要它们的初等因子一致。当F是一个代数封闭域时,F[λ]中的首项系数为1的既约多项式只能是形如(λ-α)的一次式,所以此时F上的一个n阶矩阵A的全部初等因子必为如下的一些多项式:
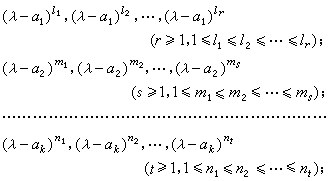 式中α1,α2,…,αk互不相同,k≥1;所有指数Л1,Л2,…,Лr,…;n1,n2,…,nt之和为n。对于每个形如
式中α1,α2,…,αk互不相同,k≥1;所有指数Л1,Л2,…,Лr,…;n1,n2,…,nt之和为n。对于每个形如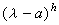 的多项式,可以惟一确定一个所谓若尔当小块,即h阶矩阵:
的多项式,可以惟一确定一个所谓若尔当小块,即h阶矩阵: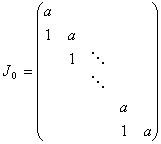 ,它只有一个初等因子,而且就是
,它只有一个初等因子,而且就是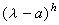 。设上述n阶矩阵A的全部初等因子的若尔当小块分别是J1,J2,…,Jυ,v=r+s+…+t,用这v个小块来合成一个n阶对角分块矩阵
。设上述n阶矩阵A的全部初等因子的若尔当小块分别是J1,J2,…,Jυ,v=r+s+…+t,用这v个小块来合成一个n阶对角分块矩阵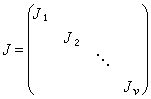 。于是A~J,而且除诸小块的次序外,J是由A所惟一确定的。J 称为A的若尔当标准形式。由此可知,只要找出A的全部初等因子即可求得A的若尔当标准形式。要找出A的全部初等因子有一个较简捷的方法,即不必把λI-A化成法式,而先把λI-A通过初等变换化成对角矩阵,其对角线上的全部多项式不一定恰是A的全部不变因子,只要将其中每个非常数多项式的首项系数化为 1,再分解因子,即可象从不变因子求出初等因子那样得出A 的全部初等因子。
。于是A~J,而且除诸小块的次序外,J是由A所惟一确定的。J 称为A的若尔当标准形式。由此可知,只要找出A的全部初等因子即可求得A的若尔当标准形式。要找出A的全部初等因子有一个较简捷的方法,即不必把λI-A化成法式,而先把λI-A通过初等变换化成对角矩阵,其对角线上的全部多项式不一定恰是A的全部不变因子,只要将其中每个非常数多项式的首项系数化为 1,再分解因子,即可象从不变因子求出初等因子那样得出A 的全部初等因子。设N是任意域F上的一个方阵,若有正整数m使Nm=0,则N称为一个幂零矩阵。例如,把上述若尔当小块中的α全换成0得出的h阶矩阵N,就是一个幂零矩阵,因为Nh=0。
若F上的方阵K具有性质K 2=K,则称K为一个幂等矩阵。例如单位矩阵就是一个幂等矩阵。由直接计算可知,对F上任意多项式ƒ(λ),有
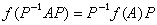 。因此,与幂零矩阵相似的矩阵仍为幂零矩阵;与幂等矩阵相似的矩阵仍为幂等矩阵。
。因此,与幂零矩阵相似的矩阵仍为幂零矩阵;与幂等矩阵相似的矩阵仍为幂等矩阵。实数域上一个非奇异矩阵T若具有性质T′=T-1(T′是T 的转置矩阵),则称为一个正交矩阵。例如解析几何里直角坐标旋转公式的系数矩阵就是正交矩阵。一个正交矩阵的转置矩阵(即其逆矩阵)仍为正交矩阵;两个同阶的正交矩阵的积仍为正交矩阵。实数域上任意一个对称矩阵A,恒可通过适当的正交矩阵T而相似于对角矩阵D,即D=T-1AT=T′AT,且D 的对角线上的实数就是A的全部特征根。
复数域上的一个非奇异矩阵U 若具有性质ū ′=U-1或U′=(ū)-1(ū ′为U 的共轭转置矩阵),就称为一个酉矩阵。一个酉矩阵的共轭矩阵仍为酉矩阵;一个酉矩阵的转置矩阵仍为酉矩阵;一个酉矩阵的共轭转置矩阵(即其逆矩阵)仍为酉矩阵;两个同阶的酉矩阵的积仍为酉矩阵。复数域上凡满足
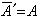 的矩阵A,称为埃尔米特矩阵。实对称矩阵作为复数域上的矩阵时,就是埃尔米特矩阵。任意一个埃尔米特矩阵A,恒可通过适当的酉矩阵U 而相似于实对角矩阵D,即D =U′Aū,且D 的对角线元素恰为A 的全部特征根。一个正交矩阵作为复数域上的矩阵时,也是一个酉矩阵。
的矩阵A,称为埃尔米特矩阵。实对称矩阵作为复数域上的矩阵时,就是埃尔米特矩阵。任意一个埃尔米特矩阵A,恒可通过适当的酉矩阵U 而相似于实对角矩阵D,即D =U′Aū,且D 的对角线元素恰为A 的全部特征根。一个正交矩阵作为复数域上的矩阵时,也是一个酉矩阵。矩阵的合同 当矩阵A经过若干套初等变换而化为矩阵B 时,则称为A合同于B,记为
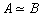 。矩阵之间的这个关系具有反身性、对称性和传递性,所以它是一种等价关系。矩阵的合同是在讨论用(对称)矩阵表示二次型的问题中产生的。
。矩阵之间的这个关系具有反身性、对称性和传递性,所以它是一种等价关系。矩阵的合同是在讨论用(对称)矩阵表示二次型的问题中产生的。所谓一套初等变换,是指将某一种初等变换首先对一个矩阵的第i列(行)施行而得一矩阵,然后再对此所得矩阵的第i行(列)施行又得一矩阵。第一、二、三套初等交换,分别由第一、二、三种初等变换组成。
两个n阶矩阵A与B 合同,必要而且只要有非奇异矩阵P 使P′AP =B。与对称矩阵合同之矩阵仍为对称矩阵。每个秩数为r的实对称矩阵A恒合同于一个对角矩阵,其对角线上有p个1与q个-1;其他的对角线元素均为0,这里p≥0,q≥0,p+q=r,而且p与q都是由A所惟一确定的。实对称矩阵的特征根恒为实数。实对称矩阵A 能合同于而又相似于一个对角矩阵,其对角线元素恰为A的全部特征根。与单位矩阵合同的实对称矩阵,称为正定矩阵。对于n阶实对称矩阵A,以下命题是等价的:A为正定矩阵;有非奇异矩阵Q使
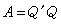 ;A的所有主子式均为正实数;A的所有i阶主子式之和Si均为正实数(i=1,2,…,n);A的所有左上角的主子式均为正实数;A的所有特征根均为正实数;A所相应的二次型为正定型。
;A的所有主子式均为正实数;A的所有i阶主子式之和Si均为正实数(i=1,2,…,n);A的所有左上角的主子式均为正实数;A的所有特征根均为正实数;A所相应的二次型为正定型。对一个复数方阵施以第一套初等变换,就是用不为零的α乘i行,再用ā乘第i列;施以第二套初等变换,就是把第i行的b倍加于第j行,再用第i列的姼倍加于第j列;施以第三套初等变换仍然是互换第i和第j两行,再互换第 i和第j两列。若对复数方阵A施以上述的若干套初等变换而得方阵B,则称为A能h合同于B。矩阵的h合同关系具有反身性、对称性和传递性,所以它是一种等价关系。两个n阶复数矩阵A与B是h 合同的,必要而且只要有非奇异矩阵P 使P′A圴 =B。与埃尔米特矩阵是h 合同的矩阵仍为埃尔米特矩阵。每个埃尔米特矩阵A 恒h 合同于一个对角矩阵,其对角线上有p个1与q个-1,其他元素均为0,这里p≥0,q≥0,p +q为A的秩数,而且p、q均是由A 所惟一确定的。埃尔米特矩阵的特征根恒为实数。埃尔米特矩阵A 不仅恒能h 合同于一个对角矩阵,而且必能相似于一个对角矩阵,此时其对角线元素恰为A的全部特征根。与单位矩阵是h合同的埃尔米特矩阵,称为正定埃尔米特矩阵。对于一个n阶埃尔米特矩阵A,以下命题是等价的:A 为正定埃尔米特矩阵;有非奇异矩阵Q 使
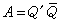 ;A的所有主子式为正实数;A 的所有i阶主子式之和Si,均为正实数(i=1,2,…,n);A的所有左上角的主子式均为正实数;A的所有特征根均为正实数;A所相应的埃尔米特二次型是正定埃尔米特二次型。复数域上的一个方阵A若满足A凴′=凴′A(即A与凴′可交换)就称A为正规矩阵。实对称矩阵、埃尔米特矩阵、正交矩阵与酉矩阵都是正规矩阵。每个复数方阵A均可表为A=h1+ih2,其中h1与h2均为由A 所惟一确定的埃尔米特矩阵,此时A为正规矩阵必要而且只要h1与h2可交换。正规矩阵A与凴′有相同的特征向量。一个复数方阵A为正规矩阵,必要而且只要有酉矩阵U 使U-1AU 为对角矩阵。
;A的所有主子式为正实数;A 的所有i阶主子式之和Si,均为正实数(i=1,2,…,n);A的所有左上角的主子式均为正实数;A的所有特征根均为正实数;A所相应的埃尔米特二次型是正定埃尔米特二次型。复数域上的一个方阵A若满足A凴′=凴′A(即A与凴′可交换)就称A为正规矩阵。实对称矩阵、埃尔米特矩阵、正交矩阵与酉矩阵都是正规矩阵。每个复数方阵A均可表为A=h1+ih2,其中h1与h2均为由A 所惟一确定的埃尔米特矩阵,此时A为正规矩阵必要而且只要h1与h2可交换。正规矩阵A与凴′有相同的特征向量。一个复数方阵A为正规矩阵,必要而且只要有酉矩阵U 使U-1AU 为对角矩阵。矩阵的理论起源,可追溯到18世纪,见于著作则是在19世纪。A.凯莱在1858年引进矩阵为一个正方形的排列表,且能进行加法与乘法运算,于是人们就把A.凯莱作为矩阵论的创始人。然而在此之前,C.F.高斯在1801年与F.G.M.艾森斯坦在1844~1852年就早已先后把一个线性替换(即线性变换)的全部系数作为一个整体,并用一个字母来表示。艾森斯坦还强调乘法的次序的重要性,指出ST与TS未必相同。与艾森斯坦同时的C.埃尔米特以及稍后的E.N.拉盖尔和F.G.弗罗贝尼乌斯也都先后发展了线性替换的符号代数。弗罗贝尼乌斯较丰富的工作于1877年发表在最早的数学杂志之一的《克雷尔杂志》上。矩阵的相似标准形,矩阵的合同标准形,矩阵的求逆,矩阵的特征值与广义特征值等是矩阵论的经典内容;矩阵方程论,矩阵分解论,广义逆矩阵等是矩阵论的现代内容。矩阵及其理论在现代科学技术的各个领域都有广泛的应用。