向量(卷名：数学)
vector
一种既有大小又有方向的量。又称为矢量。例如在物理学中的速度、加速度、力等等就是这样的量。舍弃实际含义，就抽象为数学中的概念──向量。
下面限于三维欧氏空间中来讨论。
向量的表示法 通常可以用几何的或代数的方法来表示向量。
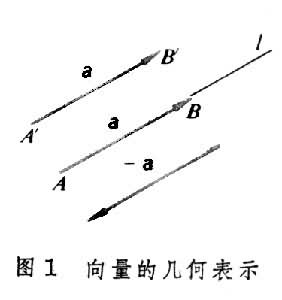
向量的几何表示法 从空间中任意一点 A出发引一半射线l，并在其上另取一点B，则有向线段AB就代表一向量（图1
），简记为
，或用α表示；这向量的大小就是线段AB的长，其方向就是半射线l的方向。向量α的大小称为它的模或绝对值，记为
。一般说来，如果向量
的起点A换作另一点A′，终点也换作另一点B′，使AB∥A′B′，且它们的指向也相同，又长度
则认为向量
与向量
是相等或相同的向量：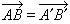
，仍可记为α。这样理解的向量有时也称为自由向量（起点可自由改变）。当然根据实际情况，有时向量的起点不能随便改变（例如，如果向量α代表一个力，其起点A代表力的作用点，这时起点就不能随意改变），这种向量有时称为固端向量。这里一般只考虑自由向量。一种特殊情况须加注意，就是B=A的情况，这时向量
称为零向量，记为0。零向量的模为0，而且无确定方向。按照前面自由向量的观点，规定两向量α，b相等的充分必要条件是：｜α｜=｜b｜，且(如果它们不是零向量)α，b的方向（包括指向）相同。
如果向量α，b（都≠0）所在直线平行或重合，则称α与b平行，记作α∥b。向量－α指的是其模与α的模相等、且与α平行但指向相反的向量。如果向量α，b所在直线互相垂直，则称α与b互相垂直或正交，记作α⊥b。
此外还规定，任何向量α都与零向量0既平行又垂直。
根据定义，任何向量α与它自身平行。
如果向量α的模等于1(｜α｜=1)，则称α为一单位向量。
向量的代数表示法 向量的几何表示法既直观又简单。但作为一种数学量，向量要参加运算，这种表示法有时就极不方便。下面向量的代数表示法就可克服这一困难。
在空间取定一右手坐标系（当然也可取左手坐标系，但为确定起见，不取左手系），如图2
。已给一向量α。把它的起点取在坐标原点O处，其终点为
。把有向线段Op投影到三坐标轴x，y，z上，分别得投影Op1，Op2，Op3，它们的有向长x，y，z分别称为α在x轴、y轴、z轴上的三个分量，而把α表示为
(1)这便是向量α的代数表示法。(x，y，z)实际上就是p点在Oxyz坐标系中的坐标。反过来，给定空间一点p (x，y，z)，由(1)式就可定义一向量α，使其三个分量依次为x，y，z。零向量0的三个分量都是0：0={0，0，0}。
由定义还可知，如果向量α以(1)式给出，则
如果向量α的起点取在Q1{x1，y1，z1}点，而终点为Q2{x2，y2，z2}，则其代数表示为
(2)当坐标系作平移时，向量的代数表示不变。当坐标系在讨论过程中始终固定不变时，则也可把(1)式，即三个有顺序的数x，y，z作为向量的定义。
向量的代数运算 向量作为一种数学量可以进行某些代数运算，如加法、减法、乘法等。这些运算方法都有实际背景，因此在实际上是有意义的，应用时是有效的。
向量的数乘 向量α与一（实）数с的乘法规定如下：定义сα为一向量，其模
且与α平行；当с>0时，其指向与α的相同；当с<0时，它就与α的相反（图3）。
当然с=0时，0α=0。特别，易见
如果用代数表示法，则若α={x，y，z}，便有
向量的数乘是符合结合律的，即若α为一向量，b，с为任二数，则
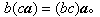
向量的加法 已给二向量α，b，来定义α+b。用几何表示法，将
取在同一起点O(图4
)，然后以OA，OB为邻边作一平行四边形，得另一顶点C(图4)，则向量c=OC就定义为α+b。所以向量的加法规则也称作平行四边形规则。又因
所以α+b也可这样来理解：先作出
然后以A为起点，作
则三角形OAC的第三条边OC就形成一向量
因此，向量的加法规则有时也称为三角形规则。如果用代数表示法，设
则有
由向量加法定义，有以下规律：
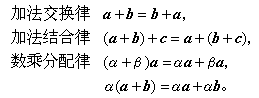
向量的减法 与通常算术中一样，把向量的减法作为加法的逆运算来定义。即已给二向量α，b，定义α-b=c为一向量，使得b+c=α。
在几何上，如果
，则
(图5
)。在代数上，如
则
由此立刻知道，α-b是惟一的。而且容易看出，
总之，对于向量的加减法和数乘来说，可以如同数字的算术运算那样进行。
向量与向量的乘法情况稍为复杂一点。
向量的内积 设有二向量α，b。先假定它们都不是零向量。记它们之间(即它们所在直线之间)的夹角为θ，则定义
为α，b的内积，或称为点积，也简记为αb。它不再是向量，而是一个数，所以也称为数积。如果α，b中只要有一个是零向量，则定义α·b=0。如果用代数方法，设
则
由定义还可看出α·α(也记为α2)=｜α｜2=α2（α仍表示α的模）。
向量的内积遵从以下一些运算规则：
此外，还可看出，两向量α，b互相垂直（正交）的充分必要条件为α·b=0（不论α，b是不是零向量）。向量的外积 这是向量的另一种乘法。仍设α，b为二向量。也暂先假定它们都不是零向量，且不平行。定义α×b=c为一向量，其模为
|c|=|α×b|=|α||b||sinθ|， (3)式中θ仍为α，b的夹角，其方向要求与α，b都垂直，而其指向如下法规定：使α，b，c的指向依次恰如Oxyz坐标系中x轴，y轴，z轴的正向那样构成一右手系（图6
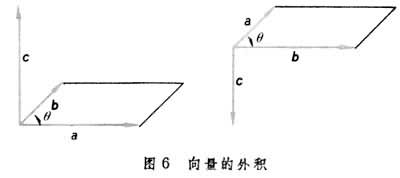）。｜α×b｜在几何上正好是以α，b为两邻边构成的平行四边形的面积。如果α∥b，则因θ=0或π，故定义α×b=0；因此，如果α，b中至少有一个是零向量，则也有α×b=0。α×b称为α，b的外积或叉积。因为它仍是个向量，所以也称为向量积。用代数表示法时，设
则α×b={α2b3-α3b2，α3b1-α1b3，α1b2-α2b1}。
注意，向量外积不服从交换律，而服从反交换律：
它也不服从结合律，即一般
但若注意了次序不能改变，则这一乘法却服从分配律：
两向量α，b平行的充分必要条件是α×b=0。值得注意，对于任意向量α，恒有α×α=0。
向量的外积与内积间有下一重要公式：
向量的混合积 下面这一把向量的外积和内积结合在一起的乘积也是很有用的：(α×b)·c，称为α，b，c的混合积，也记成(α，b，c)。它是一个数而不是向量。
如果
则可以用行列式来表示混合积：
由此可见
在几何上，如果把α，b，c的起点都放在同一点O，则(α×b)·c的模表示由这三向量为邻边构成的平行六面体的体积（图7
）。向量的分解 正如力、速度等可分解为分力、分速度等等，向量也可分解为分向量，即如果α=b+c，则称α被分解为两分向量b，c。
常用的分解为：在取定坐标系后，分别记沿x轴、y轴、z轴正向的单位向量为i，j，k(图8
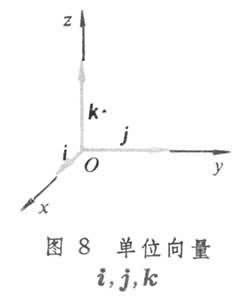)，即i＝{1，0，0}，j＝{0，1，0}，＝{0，0，1}，则任何向量α={x，y，z}可分解为
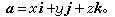注意到i，j，互相垂直，且
则也可利用上述分解式来进行向量计算，完全可按通常代数运算来进行。例如
有时只考虑位于同一平面中的向量，这时向量还可用复数来表示（见复数）。向量概念还可推广到维数更高的空间或更为抽象的空间中去。
还可考虑向量（依赖于自变量时）的微分、积分等等分析运算（见向量分析）。