模(卷名：数学)
module
在线性空间的基础上建立起来的一种代数系统，其概念至少可以追溯到19世纪L.克罗内克曾考虑的多项式环上的模。20世纪20年代末，（A.）E.诺特研究过模在表示论以及代数的结构理论上所起的作用，而使模成为代数学中的一个重要工具。20世纪40年代发展起来的同调代数，更以模为其主要的研究对象，从而对环论的发展又起了促进的作用。
把线性空间的系数域改用环U来代替就得到环U上的模。由于一般的环不是可交换的，所以模有左模与右模之分。设U为任意的一个环，X为一个加法交换群，如果有一种乘法，使得对任何α∈U，x∈X，乘积αx必属于X，而且
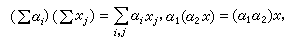那么X称为一个左U模，简称U模。特别，若U有单位元1，且1x=x，则X称为一个酉U模。如果U的元素在乘积的右边即xα，那么X称为右U模。域F上的线性空间当然是一个（双边的）F 模。环U的任一个左理想必是一个U模，特别，环U本身也是一个U模(也是右U模)。对于任一个加法交换群X，若以l(X)为其左自同态环，则X是一个左l(X)模。因为当σ∈l(X)时，可定义σx=σ(x)，故对于任意的环U，任何交换群X都可由环同态
来定义成一个U模，因为这时可取αx=ψ(α)x。假定X是一个U模，而A是X的子群，如果A也是一个U模（对同样的乘法），那么A称为X 的子模。这时，商群X/A可以作成一个U模，称为商模或差模（因X是一个加法交换群）。若A 与B 都是X的子模，则A∩B 也是X 的一个子模，而且集合{α+b│α∈A，b∈B}是A与B 的和，记为A+B，如果A+B中每一个元素表成A与B 的元素之和的表达式是惟一的，即，当α+b=α′+b′时必有α=α′，b=b′，那么此和称为直和，记为A嘰B。
以下假定所考虑的环都有单位元，而且所有的模都是酉模。设X 与Y 都是U模，如果σ 是X 到Y的群同态，而且σ(αx)＝ασ(x)，那么σ 称为一个模同态。由X 到Y的所有模同态组成之集Hom寶（X，Y）是一个加法交换群
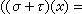
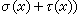。于是，以U模为对象，Hom(X，Y)为态射集，则得一个模范畴寶M。右U模的范畴常以M寶表之。由于模范畴寶M的性质实际上取决于环U，因此，模论也是研究环的一个重要工具。单模 如果除了0与X 本身以外，X 没有其他的子模，那么X 称为一个单模。例如，若P是U的极大左理想，则商模U/P是一个单模，而且任何单模都取此形式。一些（有限或无穷多个）单模的直和称为半单模。
若X是单模，则Hom(X，X)是一个体D。这就是许尔引理。因此，X可视为D上的线性空间，而且每一个α∈U都对应于这个空间的一个线性变换，把这个空间的所有线性变换定义成某一个拓扑空间T，N.雅各布森曾证明U在T 中是处处稠密的。用代数的语言来表达稠密性定理，即为，对任意n个D上线性无关的模元素x1，x2，…，xn，与任意的n个模元素y1，y2，…，yn，必有一个α∈U，使αxi=yi(i=1，2，…，n)。
单模在环论中是起着一定的作用的，例如，具有忠实单模X 的环U，称为本原环。所谓忠实模，是指αX=0时必有α=0。在雅各布森意义下的半单环是本原环的次直和。
诺特模与阿廷模 设X为一个U模，如果X 的任何一些子模之集S 都有一个极小的模A，它不包含S 中任何其他的模，那么X 称为一个阿廷模。如果任何一些子模之集S一定有一个极大的模B，它不包含在S 的任何其他的模内，那么X 称为一个诺特模。
一个U模C 称为不可分解模，是指它不是C 的两个真子模的直和。
若X 既是一个阿廷模，又是一个诺特模，则X 可分解成有限个不可分解模的直和，而在某种同构的意义下，此分解式是惟一的。这就是著名的克鲁尔－雷马克－施密特定理。
自由模与投射模 设X为U模，若X有子集
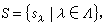
使X 中的每一个元x 都可表为如下形式
(1)则S 称为X 的一个生成系。若Λ为单元集合，则X 称为一个循环模。若(1)中的αi都是惟一的，则X 称为一个定义于集合S上的自由模。当S为任一个非空集合时，所有如(1)的形式也组成一个自由模。任何模A都是一个自由模的同态象，因为若取｛αλ｝为A的一个生成系，再取一个抽象集合 S={sλ}与｛αλ｝一一对应，让F 为定义于S上的自由模，于是让ψ:F→A使得
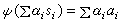，即得满同态。取K=Kerψ，得短正合列
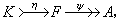(2)其中“
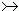”表单同态（或嵌入映射），“
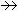”表满同态。这个性质表达了自由模在模论与同调代数中所起的主要作用。对于同一个A，(2)中的F并不惟一，可能会出现这样的现象：对于某一个F，其相应的K是自由的，但对于另外的一个F，相应的K却不是自由的（当然可能所有的K都不自由）。但是，如果放宽条件，把自由模改成投射模，那么就不仅每一个A 都是一个投射模P 的同态像，而且不同的P 所对应的K 或者全部都是投射模，或者全都不是投射模。
如果对于任何U模B，任何模同态σ:P→B，以及任何满同态π:C
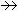B，恒有ƒ:P→C，使πƒ=σ，即可交换，那么P 称为一个投射模(图1
)。不难证明以下四种叙述是等价的：①P是投射模；②对任何满同态C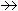
P 必有Q ，使
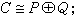③
时，P1与P2均为投射模;④有P′及自由模F，使F=P嘰P′。这些等价叙述刻画了投射模的基本性质，特别，由④可知，自由模必是投射模。因此，对每一个A，必有投射模P，使得有短正合列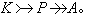
，故K与K′或者都是投射模，或者都不是投射模。正是由于这个性质，才使投射模在模论与同调代数中处于特殊重要的地位，而在模与环的研究中起着极其重要的作用。内射模 这是一个与投射模相对偶的概念，只要将图1中
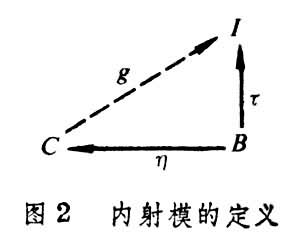所有的箭头都调转方向，“满”改为“单”即得内射模的定义，如图2所示。于是，I是内射模；对任何单同态I 
C 必有J使 
；当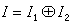
时，I1与I2都是内射模;这三种说法是等价的。此外，任何U模A都可嵌入到一个内射U模中，即有内射表现
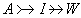。 (5)与投射模的情况一样，如果另有一个内射表现
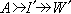，则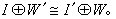
因此，内射模在模论与同调代数中的某些方面也将起着与投射模相类似的作用。对偶模与自反模 设A为U模，把U本身也看成一个U模，则Hom(A，U)是一个加法交换群。若在
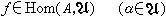
时，定义(ƒα)(α)=ƒ(α)α ∈U，则ƒα∈Hom(A，U)，因此后者是一个右U模，记作A*。同样，
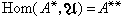可定义成一个左U模。A*通常称为A的对偶模，因而，A**是A*的对偶模。在 α∈A 时，定义
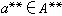，使对任何ƒ∈A*，恒有
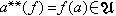，于是，让α对应α**就得出A到A**的一个自然映射φ。若φ是同构，则A是自反模。若φ是同态，则A是半自反模。模的张量积与平坦模 设A为右U模，X为左U模，G是一个加法交换群，映射φ:A×X→G称为一个线性平衡映射，是指①
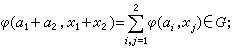②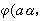
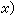
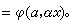假定ψ:A×X→T是一个线性平衡映射，且有泛性质，即：对任何线性平衡映射φ)：A×X→G，恒有唯一的ƒ:T→G，使得有交换图（图3
），则T称为A与X的张量积，记为
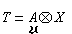或A圱X，而ψ(α，x)则记为α圱x。可以证明，A圱X 恒存在且惟一，而T=A圱X是由ψ的像所生成的。例如，若A与X依次为域K上的n维与m 维线性空间，基底依次为αi与xj，则A圱X是K上的一个nm 维线性空间，其基底可取为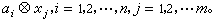
假定g:A→B是一个单同态（g的核等于0），问
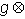1:
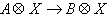使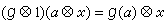 
是否一定是 单同态? 答案是否定的，即g圱1可能不是单同态。例如，设A与B 相应为由α与b所生成的无穷循环群，X是由x所生成的三元循环群(3x=0)，它们都是Z模，Z是整数环。令g:A→B，g(α)=3b，则g为单同态。由于A圱X与B圱X相应为由α圱x与b圱x 所生成的三元循环群，故α圱x≠0。但 
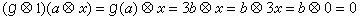，所以g圱1不是单同态。然而，在X为一个由x所生成的无穷群时，若g:A→B是单同态，则
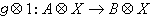仍是一个单同态。因此有如下的定义：若对任何单同态g:A→B，g圱1:A圱X→B圱X仍是单同态，则X称为一个平坦模。模表示 它的理论在群论与环论中都是非常重要的。设U与B都是环，而M既是一个左U模，又是一个右B模，且对α ∈U，m∈M.β∈B，恒有(αm)β=α(mβ)，于是有对应φ，每一个α∈U对应B模M的一个模自同态σ，αx=σx，这个对应是一个环同态φ，它称为U在B上的一个表示，M为相应的表示模。通常还要求U以B为右算子区，
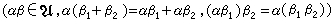，且(αβ)m=(αm)β=α(mβ)，再定义(σβ)(m)=σ(mβ)，则上述的φ为一个算子同态。例如，设G为一个群，取K为一个域，M为K上的一个线性空间。于是，群环KG 在域K上的一个表示φ，就是由KG到M的线性变换环l(M)的一个环同态。由于α∈G有逆元素，所以φ(α)是M的一个非异线性变换，因此φ给出G的一个线性表示。特别，若M是有限维线性空间，则在固定一个基底后，φ给出G的一个矩阵表示。
参考书目
T.S.Blyth，Module Theory，Clarendon Press，Oxford，1977.