模型理论(卷名：力学)
model theory
直接在结构即原型上进行的实验，称为原型实验；在按照原型设计的模型上进行的实验，则称为模型实验。一般说来，前者比后者更为真实。但在进行研究或对新设计方案进行比较，或者由于种种原因而不能进行原型实验时，模型实验就成为重要的手段。使模型和原型相似所根据的理论，称为模型理论，它的基础是相似理论。
相似理论 相似现象的同一物理量之比，称为相似系数，或称相似比例。所有相似系数之间，存在着某种关系式，称为相似指标。与此对应，相似现象各物理量之间，也存在某种关系式，称为相似判据。
相似第一定理 相似现象用相同的方程式描述。彼此相似的现象，其相似指标等于1，其相似判据的数值相等。
相似第二定理 描述一个现象各物理量之间的关系式，都可以写成相似判据方程式。
相似第三定理 单值条件相似，且从它导出的相似判据的数值相等，是现象彼此相似的充分和必要条件。
单值条件包括：几何条件、初始条件、边界条件以及对所研究的现象有重大影响的物理条件等。对于常温静态弹性应力分析问题，主要考虑的是几何条件、载荷条件、约束条件和泊松比条件。而对运动学和动力学的问题，则还要考虑初始条件和时间条件等。在复杂的模型实验中，要求单值条件完全相似是有困难的，但应尽量保持相似。
以上是模型设计和获得相似量必须遵循的法则。
确定相似判据的方法 相似判据是根据相似理论确定的，有下述两种方法：
方程式分析法 适用于已有数学方程描述的现象。以常温静态实验应力分析为例，按弹性力学，原型的静力平衡方程为：
， (1)式中σ为正应力；τ为剪应力;ρ为密度；x、y、z为坐标。令
=σp/σm、Cl=lp/lm和Cρ=ρp/ρm分别为应力相似系数、几何尺寸相似系数和密度相似系数，l为几何量（长度等），脚标p和m分别代表原型和模型。因模型和原型相似，故依相似第一定理，其相似指标和相似判据分别为：
(2)和σ/lρ=π， (3)式(3)同时适用于原型和模型。 这里π 是不变量。根据这些公式，可以得到在体积力作用下的应力转换关系：
σp＝σm(lpρp/lmρm)。 (4)
采用光弹性法时，常以离心力场代替重力场来模拟模型的自重作用。若模型受到的离心力为ρmω2r，ω为转速，r为旋转半径，则式(4)中的ρm被ρmω2r/g（g为重力加速度）代换后，得到：
σp＝σm(lpρpg/lmρmω2r)， (5)ω2r为离心机的径向加速度。
若不考虑体积力，则
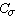/Cl为任意常数。相似指标为任意常数的情况，称为自然模型化。在不考虑体积力的实验应力分析模型中，只要模型和原型保持几何相似、载荷相似、约束条件相似和泊松比相等，则两者的应力情况相似。用同样的方法分析本问题的边界条件方程，可得出在分布载荷p作用下的应力转换关系：
σp＝σm(pp/pm)。 (6)对于集中载荷，外力P＝pl2，故有：
σp＝σm(Ppl娽/Pml婃)。 (7)
对于二维问题，因为沿板厚δ 的应力均匀分布，所以平面尺寸l和厚度可选取不同的相似系数，这时式(7)变为：
σp＝σm(Pplmδm/Pmlpδp)。 (8)
以上是分析弹性力学小位移基本方程得到的应力转换关系。
量纲分析法 这是一种广泛应用的方法，对于那些还没有数学方程的问题尤为重要。仍以常温静态应力分析问题为例：
在此情况下，应力σ和l、P、E(弹性模量)、ν（泊松比）、ρ等有关。设l为结构中的某长度，则其他长度分别为n1l，n2l，…。n1，n2，…为有关的倍数。若某外力为P，则其他外力为níP，n勶P，…。ní，n勶，…为相应的倍数。更以v1，v2，…表示外力作用方向，则得：
σ＝嗞(E，ν，l，n1l，n2l，…，P，níP，n勶P，…，
v1，v2，…，ρ)。 (9)选用E、l为基本单位，并用无量纲数表示，得：
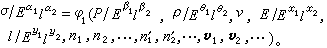(10)然而相似现象的相似判据的数值相同，即
=π1，
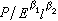＝π2，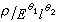
=π3，ν=π4，
＝π5，
＝π6。故可用量纲公式确定各指数。以π1为例：
，比较两边同类因子的指数，得到：α2－2α1=－2 和 α1=1。联立解得α1=1，α2=0，故有：
π1=σ/E，同样可得：
π2=P/El2 和 π3=ρl/E，而
π4=ν。
若选E和l作为基本单位，它们都等于1，则式(10)可写成：
σ/E＝嗞1(P/El2，ρl/E，ν，n1，n2，…，í$，勶$，…，
v1，v2，…)。 (11)
这就是常温静态弹性结构应力分析问题中各物理量之间的关系式，它是相似判据方程的雏形。对于没有方程式的物理现象，只要从这种雏形出发，就不难用模型实验法找出其函数关系来。
按上述的相似判据，还可得到应力的转换关系。对于不考虑 ρ的影响的模型实验，在保证几何相似、载荷相似、约束条件相似和νm=νp的前提下，依据相似理论，对于相似现象，π1和π2应同时适用于模型和原型，则得：
σp＝σm(Ep/Em) (12)和
Ep/Em=Ppl娽/Pml婃。 (13)由上两式得：
σp＝σm(Ppl娽/Pml婃)。 (14)
式(14)和用方程式分析法得到的式(7)一样。 但是，在推导式(14)时，未限制变形的大小，故式(14)也适用于非线性弹性问题，只是必须同时满足式(13)。这就是说，在选定模型材料和几何相似系数后，载荷相似系数就不能任意选择。上述的小变形问题，属于线性问题，可用叠加原理，因为这时应力、变形都和载荷成正比，故应用式(14)时不受式(13)的限制，从而在进行模型实验时，弹性模量、几何和载荷相似系数都可以任意选取。但要保证或近似保证νm=νp，否则将在不同程度上破坏三维应力的相似。
结构变态模型
对于诸如工字型、箱形等空间薄壁结构，如果主要是处于平面应力状态，则在设计和制造模型时，只须保证模型和原型的平面几何形状相似，而厚度可以改变。最简单的情况是将薄壁截面简化为任意厚度的矩形截面。这时，应力转换关系可按不同载荷形式和相应的截面几何特性来确定。对于轴向拉、压和平面弯曲，其关系式分别为：
σp＝σm(PpAm/PmAp) (15)和
σp＝σm(ΜplpIm/ΜmlmIp)， (16)式中A为横截面的面积；P为轴向力；Μ为弯矩；l为截面的形心主惯性矩。
在一定条件下，把几何相似条件放松，将三维的薄壁截面构件简化为二维的矩形截面构件，而仅保持平面几何相似的模型，称为结构变态模型。用这种模型可以避免模型制造的困难，也扩大了模型理论和模型实验的应用范围。
动态载荷相似判据
结构受动态载荷作用时，可以按模型理论求得相应物理量的转换关系。例如冲击问题，参与的物理量有物体的l、E、ν、ρ、P、σ、应力波的传播速度c、时间t以及物体碰撞时的速度变化Δv等。和处理静态载荷的方法相似，可得：
π1＝c/Δv，π2＝ct/l，π3＝σ/E，π4＝σl2/P，
π5＝v
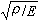，π6＝ν。若模型材料已选定，根据这些相似判据，就可得到碰撞速度、应力波传播速度、撞击力、时间以及应力的转换关系。
中国在设计大连新港输油栈桥时就曾运用模型理论对结构进行应力分析。