模糊性数学(卷名：数学)
mathematics of fuzziness
研究和处理模糊性现象的数学理论和方法。1965年美国控制理论学者 L. A.扎德发表了论文《模糊集合》（或译不分明集合、弗晰集合），标志着这门新学科的诞生。
现代数学建立在集合论的基础上。集合论的重要意义，就某一侧面看，在于它把数学的抽象能力延伸到人类认识过程的深处。一组对象确定一组属性，人们可以通过指明属性来说明概念（内涵），也可以通过指明对象来说明它。符合概念的那些对象的全体叫做这个概念的外延，外延实际上就是集合。从这个意义上说，集合可以表现概念，而集合论中的关系和运算又可以表现判断和推理，一切现实的理论系统都有可能纳入集合描述的数学框架。但是，数学的发展也是有阶段性的。经典集合论只把自己的表现力限制在那些有明确外延的概念和事物上，它明确地限定：每一个集合都必须由确定的元素所构成，元素对集合的隶属关系必须是明确的，绝不模棱两可。对于那些外延不分明的概念和事物，经典集合论是暂时不去反映的，这属于待发展的范畴。关于这一点，集合论发展的先驱之一(F.-É.-J.-) É.波莱尔就早有察觉，他曾借一个希腊悖论提出了这样一个问题：究意有多少粒种子才够得上是一堆？“一堆”这个概念的外延是什么？它是由哪些自然数所构成？“……界限在哪里？能不能说325647粒种子不叫一堆而325648粒就构成了一堆？”按照恩格斯的观点：“辩证法不知道什么绝对分明和固定不变的界限，不知道什么无条件的普遍有效的'非此即彼'”，“一切差异都在中间阶段融合，一切对立都经过中间环节而相互过渡。”秃与不秃是不能以某一头发根数来分界的，人与猿、脊椎动物与非脊椎动物、生物与非生物等等也都找不到确切的界线。从差异的一方到差异的另一方，中间经历了一个从量变到质变的逐步过渡的过程，这种现象叫做差异的中介过渡性;处于中介过渡的事物显示出亦此亦彼性质，由这种亦此亦彼性所引起的外延判断和划分上的不确定性就叫做模糊性。具有模糊性的事物和现象不能用经典集合论来刻画。
模糊性现象是一种普遍存在的现象。以前人们回避它，但是，由于现代科技所面对的系统日益复杂，模糊性总是伴随着复杂性出现；各门学科，尤其是人文、社会学科及其他“软科学”的数学化、定量化趋向把模糊性的数学处理问题推向中心地位；最重要的是，由于计算机科学的进展，要使计算机能像人脑那样对复杂事物具有识别的能力，就必须研究和处理模糊性。从经典集合论向模糊集合扩展是历史发展的要求。扎德的想法是很自然的。对论域U 中的子集A 可以通过它的特征函数ⅹA来描述：
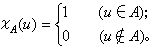扎德把ⅹA(u)叫做u对A的隶属度，ⅹA(u)=1=100％表示u百分之百地隶属于A，ⅹA(u)=0表示u不属于A，经典集合论要求隶属度非0即1，模糊集合则突破这一限制。所谓给定U 的一个模糊子集A，乃是指给定了映射 μA：U→[0，1]。μA叫做A 的隶属函数，μA(u)叫做u对A的隶属度。当μA 的值域只包含0、1二值时，A 就是一个经典集合，因而模糊集合是普通集合概念的推广。选定阈值λ（0≤λ≤1），当μA(u)≥λ时，视u为A的成员（相对于阈值λ而言），否则便不是A的成员，于是A可以用一个经典子集
来近似表示，Aλ叫做A的λ截集。当λ从1下降至0，Aλ由小变大，{Aλ}说明了A可被看作是一个“可变的”、“有弹性”的、具有“游移边界”的集合。扎德用隶属度概念来表现处于中介过渡的事物对差异一方所持有的倾向性程度，从“亦此亦彼”中提取了“非此即彼”的信息。用[0，1]中的一个实数来表示某一对象对某一概念的隶属度，这是一种抽象。那么这种抽象究竟是否正确？隶属度有客观意义吗?如何确定它?这是模糊性统计所研究的问题。波莱尔在解决“一堆”问题时，隐约显露出这样的设想：每次让人报一个区间[ξ，+∞]以表示“一堆”的一个近似的外延，ξ是一个自然数，它随人而异，随时而异。统计这些区间对某一自然数n的覆盖频率，用它可以表示 n对于“一堆”概念的符合程度。现在有一种模糊统计模型正是按照这种思想建立的。大量试验表明，类似于概率统计试验中事件发生的频率稳定性，在模糊性统计试验中也存在着覆盖频率稳定性的规律，它说明了隶属度概念是一种符合客观实际的正确抽象。模糊性统计每次试验所得到的是论域中的一个“集”，它是一种集值统计。随机性反映因果律的破缺，它是由于条件不充分而导致的关于结果发生与否的不确定性；模糊性反映排中律的破缺，它是由于外延不分明而导致的对给定事物在是非判断上的不确定性，二者是有区别的。但它们之间又有联系，这是正在深入研究的一个课题。
就像“价值“可以公度一切商品那样，在一定条件下，隶属度也可以公度一类模糊性的事物。诸如“效用度”、“满意度“等这样一些特殊的隶属度，在管理决策理论中都扮演了统一量纲、化繁为一的重要角色。隶属度具有可运算和变换的品格，这正是模糊集合论应用、发展的前提。扎德最初定义模糊集合运算如下：
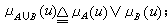
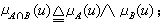
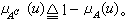式中∨、∧分别表示对实数取上、下确界的运算:α∨b＝
，A∪B、A∩B分别叫A、B的并与交，Ac叫A的补集。当A、B蜕化成经典集合时，上述运算就是经典的集运算，所以上述模糊性集运算是经典集运算的进一步推广。但是这种推广不是惟一的，已有十几种不同的模糊性集运算定义，研究各种运算的特性、适应条件、相互关系，这是“模糊算子理论”所研究的内容。隶属度就是一个模糊性命题的真确程度，隶属度运算联系着逻辑的真值演算。布尔逻辑的真值域是({0，1}，∨，∧)，它是一个布尔代数。扎德集运算所对应的是一种连续值逻辑，其真值域是([0，1]，∨，∧)；它不再是一个布尔代数，因为它不再满足互余律:α∨αc=1，α∧αc=0（对所有α∈[0，1]），互余律反映了布尔逻辑的“非此即彼”性质。([0，1]，∨，∧)叫做软代数。软代数有什么代数性质?当以([0，1]，∨，∧)取代({0，1}，∨，∧)时，布尔逻辑会变成什么样子？更一般地，以(P([0，1])，∨，∧)取代（这时得到模糊语言值逻辑），又会得到什么结果？这里P(U)表示由U 的一切子集构成的集合，P([0，1])中的∨、 ∧按并、交运算定义。这些构成了“模糊逻辑代数”理论。格论是它特别重要的工具。
笛卡儿乘积U×V（见多重线性代数）的模糊子集R叫做从U 到V 的模糊关系。模糊关系在模糊集合的理论中占有比普通关系在普通集合论中更为重要的地位。设R、S分别是从U 到V、从V 到W 的模糊关系，定义合成关系R。S为：
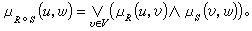当R，S 蜕化为普通关系时，上式变为普通关系的合成。若只考虑U、V、W为有限论域的情形，则模糊关系可以用元素在[0，1]中的矩阵来表示，而关系的合成转化为下面这样的矩阵乘法：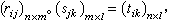
。这叫做矩阵的模糊乘法。它与普通矩阵乘法步骤一样，只是将实数乘法“·”改为“∧”，把“+”改为“∨”。一个有实用价值的理论问题是求解x=(x1，x2，…，xn)使满足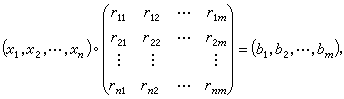
也叫做求解模糊线性方程组。它的解结构比普通线性方程组复杂。现已证明，任一模糊线性方程组若有解则必有惟一的最大解
其中
但是不一定存在最小解，寻求全体极小解的各种解法和程序已经基本给出。类似一些问题都归结到这样一点：若以([0，1]，∨，∧)代替实数域(R，+，·)，将出现什么样的线性代数理论？([0，1]，∨，∧)是半环，∨，∧均无逆运算，因而问题变得复杂化，但仍有一些特有的性质和规律。这些便构成了“模糊线性代数”、“模糊矩阵理论”的研究内容。从纯数学角度看，集合概念的扩充使许多数学分支都增添了新的内容。例如不分明拓扑、不分明线性空间、模糊测度与积分、模糊群、模糊范畴、模糊图论，等等。其中有些领域，尤其是不分明拓扑，已有比较深刻的研究内容，为由来已久的格上拓扑学提供了新的背景与方法。
模糊性数学发展的主流是在它的应用方面。既然模糊性概念已经找到了模糊集的刻画方式，那么人类运用概念进行判断、评价、推理、规划、决策和控制的过程也可以用模糊性数学的方法来逐步刻画。例如，“模糊聚类分析”给出利用模糊关系来对事物进行模糊性划分的方法；“模糊模型识别”给出了模糊性事物的识别方法；“模糊综合评判”在多因素场合给出了对事物进行评定的方法；“模糊规划”给出了模糊性限制条件下的规划模型与解法；“模糊决策”给出了多目标情形下能反映决策者意志与经验的决策方法；“模糊控制”给出了模糊性系统当精确数学模型难以建立而又有人的实际控制经验可以采纳时的控制方法。这些方法构成了一种模糊性系统理论，构成了一种思辨数学的雏形。它已经在医学、气象、结构力学、心理、经济管理、计量、石油、地质、环境、生物、农业、林业、化工、纺织、语言、控制、遥感、雷达、教育、体育等等方面有了应用。在气象、结构力学、控制、心理等方面已有具体的研究成果说明模糊性数学是该领域中的一项重要的数学工具。然而，模糊性数学最重要的应用领域是计算机智能。它已经被运用于专家系统和知识工程等方面。不少人认为它与新一代计算机的研制有紧密的联系。
模糊性数学还没有成熟，对它也还存在着不同的意见和看法，有待实践去检验。
参考书目
C.V.尼古塔、D.A.拉莱斯库著，汪浩、沙钰译，《模糊集合在系统分析中的应用》，湖南科学技术出版社，长沙，1981。(C.V.Negoitǎ and D.A.Ralescu，Applications of Fuzzy Sets to Systems Analysis，Birkhuser， Basel， 1975.)
L.A.扎德著，陈国权译，《模糊集合·语言变量及模糊逻辑》，科学出版社，北京，1982。(L.A.Zadeh The Concept of a Linguistic variable and Its Application toApproxiMate Reasoning，Elsevier，New York，1975.)
汪培庄编：《模糊集合论及其应用》，上海科学技术出版社，上海，1983。