策略迭代法(卷名：数学)
policy iteration method
动态规划中求最优策略的基本方法之一。它借助于动态规划基本方程，交替使用“求值计算”和“策略改进”两个步骤，求出逐次改进的、最终达到或收敛于最优策略的策略序列。
例如，在最短路径问题中，设给定M个点1，2，…，M。点M是目的点，сij>0是点i到点j的距离i≠j，сij=0，i，j=1，2，…，M，要求出点i到点M的最短路。记ƒ(i)为从i到M的最短路长度。此问题的动态规划基本方程为
(1)其策略迭代法的程序如下：选定一初始策略u0(i)，在这问题中，策略u(i)的意义是从点i出发走一步后到达的点，而且作为策略，它是集{1，2，…，M-1}上的函数。由u0(i)解下列方程组求出相应的值函数ƒ0(i)：
再由ƒ0(i)求改进的一次迭代策略u1(i)，使它是下列最小值问题的解：
然后，再如前面一样，由u1(i)求出相应的值函数ƒ1(i)，并由ƒ1(i)求得改进的二次迭代策略u2(i)，如此继续下去。 可见求解(1)的策略迭代法的程序由下列两个基本步骤组成：①求值计算 由策略 un(i)求相应的值函数ƒn(i)，即求下列方程的解：
②策略改进 由值函数ƒn(i)求改进的策略，即求下列最小值问题的解：
式中规定，如un(i)是上一问题的解，则取un+1(i)=un(i)。在一定条件下，由任选的初始策略出发，轮换进行这两个步骤， 经有限步N后将得出对所有i，uN+1(i)=uN(i)这样求得的uN(i)就是最优策略，相应的值函数ƒN(i)。是方程(1)的解。
对于更一般形式的动态规划基本方程
(2)这里ƒ，H，φ为给定实函数。上述两个步骤变成：①求值计算 由策略un(x)求相应的值函数 ƒn(x)，即求方程
之解，n=0，1，2…。②策略改进 由值函数ƒn(x)求改进的策略un+1(x)，即求最优值问题
的解。对于满足适当条件的方程(2)和初始策略，上述两个步骤的解存在，并且在一定条件下，当n→
时，所得序列{ƒn(x)}与{un(x)}在某种意义下分别收敛于(2)的解和最优策略。策略迭代法最初是由R.贝尔曼提出的。1960年，R.A.霍华德对于一种马尔可夫决策过程模型，提出了适用的策略迭代法，给出了相应的收敛性证明。后来，发现策略迭代法和牛顿迭代法在一定条件下的等价性，于是，从算子方程的牛顿逼近法的角度去研究策略迭代法，得到了发展。
对于范围很广的一类马尔可夫决策过程，其动态规划基本方程可以写成
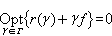；式中ƒ∈V，对所有 γ∈Γ:r(γ)∈V，γ为 V→V的线性算子，Γ为这种算子的族，而V 则是由指标值函数所构造的函数空间。假设
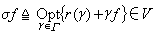当 ƒ(γ)是方程 r(γ)＋γƒ＝0 的解时， 它是对应于策略γ的指标值函数。最优策略 γ
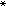定义为最优值问题
的解。这时由策略迭代法所求得的序列 {ƒn}和{γn}满足下列关系
其中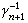
为 γn+1的逆算子。当σ是加托可微时， γn+1是σ在ƒn处的加托导数。于是，上面的关系恰好表达了牛顿迭代法在算子方程中的推广。