递归函数(卷名：数学)
recursive function
数论函数的一种，其定义域与值域都是自然数集，只是由于构作函数方法的不同而有别于其他的函数。处处有定义的函数叫做全函数，未必处处有定义的函数叫做部分函数。最简单又最基本的函数有三个:零函数O(x)=0(其值恒为0);射影函数
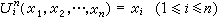；后继函数S(x)=x+1。它们合称初始函数。要想由旧函数作出新函数，必须使用各种算子。代入（又名复合或叠置）是最简单又最重要的造新函数的算子，其一般形状是：由一个m元函数ƒ与m个n元函数 g1，g2，…，gm 造成新函数 ƒ (g1(x1，x2，…，xn)，g2(x1，x2，…，xn)，…，gm(x1，x2，…，xn))，亦可记为ƒ(g1，g2，…，gm)(x1，x2，…，xn)。另一个造新函数的算子是原始递归式。具有n个参数u1，u2，…，un的原始递归式为：
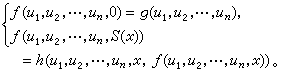具有一个参数的原始递归式可简写为：
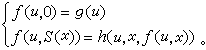其特点是，不能由g、h两函数直接计算新函数的一般值ƒ(u，x)，而只能依次计算ƒ(u，0)，ƒ(u，1)，ƒ(u，2)，…；但只要依次计算，必能把任何一个ƒ(u，x)值都算出来。换句话说只要g，h为全函数且可计算，则新函数f也是全函数且可计算。由初始函数出发，经过有限次的代入与原始递归式而作出的函数叫做原始递归函数。由于初始函数显然是全函数且可计算，故原始递归函数都是全函数且可计算。通常使用的数论函数全是原始递归函数，可见原始递归函数是包括很广的。但是W.阿克曼证明了，可以作出一个可计算的全函数，它不是原始递归的。经过后人改进后，这个函数可写为如下定义的阿克曼函数：
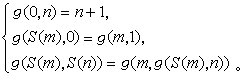容易看出，这个函数是处处可计算的。任给m，n的值，如果m为0，可由第一式算出；如果m不为0而n为0，可由第二式化归为求g(m，1)的值，这时第一变目减少了；如果m，n均不为0，根据第三式可先计算g(m，n-1)，设为α，再计算g(m-1，α)，前者第二变目减少（第一变目不变），后者第一变目减少。极易用归纳法证得，这样一步一步地化归，最后必然化归到第一变目为0，从而可用第一式计算。所以这个函数是处处可计算的。此外又容易证明，对任何一个一元原始递归函数ƒ(x)，永远可找出一数α使得ƒ(x)<g(α，x)。这样，g(x，x)+1便不是原始递归函数，否则将可找出一数b使得g(x，x)+1<g(b，x)。令x=b，即得g(b，b)+1<g(b，b)，而这是不可能的。另一个重要的造新函数的算子是造逆函数的算子，例如，由加法而造减法，由乘法造除法等。一般，设已有函数ƒ(u，x)，就x解方程ƒ(u，x)=t，可得x=g(u，t)。这时函数g叫做ƒ的逆函数。至于解一般方程ƒ(u，t，x)=0而得x＝g(u，t)可以看作求逆函数的推广。解方程可以看作使用求根算子。ƒ(u，t，x)=0的最小x根（如果有根的话），记为μx[ƒ(u，t，x)=0]。当方程没有根时，则认为μx[ƒ(u，t，x)=0]没有定义。可见，即使ƒ(u，t，x)处处有定义且可计算，但使用求根算子后所得的函数μx[ƒ(u，t，x)=0]仍不是全函数，可为部分函数。但只要它有定义，那就必然可以计算。这算子称为μ算子。如果ƒ(u，t，x)本身便是部分函数，则 μx[ƒ(u，t，x)=0]的意义是：当ƒ(u，t，n)可计算且其值为0，而x<n时ƒ(u，t，x)均可计算而其值非0，则 μx[ƒ(u，t，x)=0]指n；其他情况则作为无定义。例如，如果ƒ(u，t，x)=0根本没有根，或者虽然知道有一根为n，但ƒ(u，t，n-1)不可计算，那么 μx[ƒ(u，t，x)=0]都作为没有定义。在这样定义后，只要 μx[ƒ(u，t，x)=0]有值便必可计算。由初始函数出发，经过有穷次使用代入、原始递归式与 μ算子而作成的函数叫做部分递归函数，处处有定义的部分递归函数称为全递归函数，或一般递归函数。
原始递归函数类里还有一个重要的子类称为初等函数类，它是由非负整数与变元经过有穷次加、算术减（即｜α-b｜）、乘、算术除
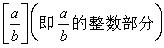、叠加Σ、叠乘П而得的函数组成的类。波兰人A.格热高契克把原始递归函数类按定义的复杂程度来分类，称为格热高契克分层或波兰分层。
要把递归函数应用于谓词，首先要定义谓词的特征函数。谓词R(x，y)的特征函数是
称谓词R 是递归谓词，若R 的特征函数是递归函数；称自然数子集A为递归集，若谓词x∈A是递归谓词。有了上述定义，就可以用递归函数来处理递归谓词和递归集。为了处理N×N（其中N 为自然数集）的子集，就要建立配对函数，所谓配对函数通常是指由N×N 到N 的一个函数ƒ(x，y)与它的逆函数g1(z)，g2(z)。它们都满足以下关系：
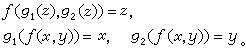可以构造许多原始递归的配对函数。递归函数也可以用来处理符号串。处理的办法是对符号及符号串配以自然数。这方法是K.哥德尔开始引进的，因此称为哥德尔配数法。例如，在要处理的符号系统｛α1，α2，α3，…｝中，可以用奇数1，3，5，7，…作为α1，α2，α3，α4，…的配数，符号串
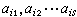以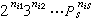
为其配数，其中Ps是第s个素数，nij是αij的配数。这种配数称为哥德尔配数。有了哥德尔配数法，就可以用递归函数来描写、处理有关符号串的谓词了。