系综(卷名：物理学)
ensemble
处在一定宏观条件下，大量性质和结构完全相同的系统的集合。又称统计系综。统计物理学研究的对象是由大数量粒子组成的宏观的物理系统，它具有同力学规律性本质上不同的统计规律性。系综是采用统计方法描述系统的统计规律性时引入的一个最基本的概念。
经典统计中，时刻t处在相宇体积元dp1…dpdq1…dq＝dpdq中的系统代表点数为ρ(p，q，t)dpdq，ρ(p，q，t)是代表点在相宇中的分布密度。
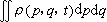是代表点的总和。这些不同的代表点代表了系统的不同运动状态，也可以把它们看作是性质和结构相同而初始条件不同的系统所处的状态。这些系统的集合就是系综。统计系综的各个系统反映了实际系统在不同时刻的面貌。它们在相空间中都沿着一定的轨道互相独立地运动着。系统的微观量L(p，q)在所有可能的微观状态上的平均值
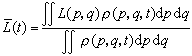，就是微观量L(p，q)在统计系综上的平均值。若使分布函数归一化
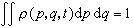，则有
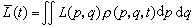。量子统计中，所研究的是混合系综，它所属的各个系统分布于一系列的量子态上。系综中任何一个系统都处在其余系统所组成的媒质之中。系统的微观状态是不连续的量子态，微观量 L也只能在各个量子态才具有一定的数值。以Lj表示系统的微观量在量子态j上的数值，ρj(t)表示系综在第 j个量子态的几率〔相当于经典统计中的ρ(p，q，t)dpdq〕，微观量L在一切可能的微观状态上的平均值就是
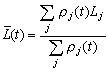，若使
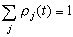，则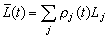
。它就是量子统计中同微观量L对应的宏观物理量。平衡态统计物理学主要考虑处于平衡状态的系统，此时，系统的宏观性质不随时间改变，于是分布函数不显含时间。系综的方法可用于由彼此存在相互作用的大数量粒子所组成的系统，按系统所处的不同宏观条件，应当采用不同的系综及其对应的不同形式的分布函数。统计方法的特点是由微观量求宏观量，在求平均值时就必须知道系综的分布函数。平衡态统计物理学常用的有微正则系综（见统计物理学）、正则系综、巨正则系综及其相应的分布。