素数分布(卷名：数学)
distribution of prime number
数论中研究素数性质的一类重要问题。素数或称质数，是指一个大于1的整数，除1和它本身外，不能被其他的正整数所整除。例如，2，3，5，7，11，13，17，19都是素数。大约在公元前300年，欧几里得就证明了素数有无穷多个。设2，3，…，p是不大于p的所有素数，q=2·3·…·p+1。容易看出q不是2，3，…，p 的倍数。由于q的最小正除数一定是素数，因此，或者q本身是一个素数，或者q可被p与q之间的某个素数所整除。所以必有一个大于p 的素数存在，由此即知素数有无穷多个。素数在自然数中占有极其重要的地位，但是它的变化非常不规则。人们至今没有找到，大概也不可能找到一个可以表示全体素数的有用公式。研究各种各样的素数分布状况，一直是数论中最重要和最有吸引力的中心问题之一。最初的研究方法，是通过观察素数表来发现素数分布的性质。现有的较完善的素数表是D.B.扎盖尔于1977年编制的，列出了不大于50000000的所有素数。从素数表可以看出：在1到100中间有25个素数，在1到1000中间有168个素数，在1000到2000中间有135个素数， 在2000到3000中间有127个素数，在3000到4000中间有120个素数，在4000到5000中间有119个素数，在5000到10000中间有560个素数。由此可看出，素数的分布越往上越稀少。目前所知道的最大素数是2216091－1(见梅森数)，它有65050位，是1985年发现的，在证明它是素数时需用特殊的方法并借助于电子计算机。关于素数分布性质的许多著名猜想，是通过数值观察、计算和初步研究提出的，大多数至今仍未解决。其中最著名的猜想有以下几个：
孪生素数猜想 两个差等于2的一对素数，称为孪生素数。例如，3和5;5和7;11和13;17和19;29和31;41和43；59和61;71和73;101和103;…;10016957和10016959；都是孪生素数。迄今所知的最大孪生素数是1159142985×22304-1和1159142985×22304+1；它们是A.O.L.阿特金和N.W.里克特于1979年得到的。所谓孪生素数猜想，即存在无穷多对孪生素数。这个猜想至今没有解决，但认为它是正确的可能性很大。在这方面的最好结果是陈景润于1966年得到的：存在无穷多个素数p，使得p+2是不超过两个素数之积。
素数定理 关于素数个数的研究是素数分布中最重要的问题之一。以 π(x)表示不大于x的素数个数，例如，π(2)=1，π(3)=2，π(100)=25，π(1000)=168。欧几里得早就证明了素数有无穷多个，即
。从表
可以看出：①x越大，π(x)与x的比值越接近于0；②x越大，π(x)与x/lnx的比值越接近于1。A.-M.勒让德和C.F.高斯猜测
即通常所称的素数定理。它是素数分布理论的中心定理。在这方面首先做出贡献的是∏.Л.切比雪夫，他在1852年左右证明了存在两个正常数с1，с2，使得不等式с1x/lnx≤π(x)≤с2x/lnx成立，其中x≥2。在1896年，J.（-S.）阿达马和C.J.de la瓦莱·普桑彼此独立而又几乎同时证明了素数定理。他们的证明都使用了高深的复变函数论知识。因此，能否以尽可能初等的方法来证明素数定理，则成为数学家一直探讨的重要问题。1949年，A.赛尔伯格和P.爱尔特希给出了素数定理的初等证明，除了极限、lnx和ex的性质之外，没有用到其他的分析知识，但证明过程十分复杂。他们的证明是基于赛尔伯格的著名恒等式：当x≥1时有
式中
表示对所有不超过x的素数求和，记号O的定义如下：设g(x)>0，ƒ(x)为一复值函数， α≤x≤b)。若存在一个与x无关的正常数M，使得当α≤x≤b)时有|ƒ(x)|≤Mg(x)，则记为ƒ(x)=O(g(x))，M称为记号O所含之常数。于是某一满足上述条件的函数ƒ(x)，就可用O(g(x))代之。有误差项的素数定理是指寻求误差π(x)-lix的最佳估计，
，它比x/lnx更接近于π(x)。C.J.de la瓦莱·普桑于1900年首先证明了
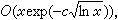这里с是一正的常数。H.von科赫于1901年在黎曼假设（见黎曼ζ函数）下证明了 
O(x1/2lnx)。И.М.维诺格拉多夫等于1958年借助于他的三角和估计方法，得到π(x)-lix=O(xexp(-с(lnx)
))，ε为任意正数，с是和ε有关的正常数。误差项π(x)-lix的变化是极不规则的。设ƒ(x)是实函数，如果存在与x无关的正常数α，使得任意大的x满足ƒ(x)>αx，则记为ƒ(x)=Ω+(x)；若使得任意大的x满足ƒ(x)<- αx，则记为ƒ(x)=Ω-(x)。若这两种情形同时出现，则记为ƒ(x)=Ω+(x)。J.E.李特尔伍德于1914年证明了：当x→∞时，有π(x)-lix =Ω+((x1/2lnlnlnx)/lnx)。算术级数中的素数定理 P.G.L.狄利克雷于1837年首先证明了首项与公差互素的算术级数中有无限多个素数。设整数q≥3.1≤l≤q，(l，q)=1。以π(x，q，l)表首项为l、公差为q的算术级数中不超过x 的素数之个数。类似于素数定理，对于固定的q，容易证明：
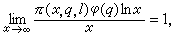式中φ(q)表示不超过q且与q互素的正整数的个数。这就是通常所说的算术级数中的素数定理。关于误差项估计，A.佩奇于1935年和C.L.西格尔与A.瓦尔菲施于1936年证明了：对任意正数h，当3≤q≤(lnx)h时，有
式中с为绝对正常数；记号O中所含的常数仅与h有关，而与q无关。算术级数中的最小素数 设k≥3，1≤l≤k，(l，k)=1。以p(k，l)表算术级数kn+l(n=0，1，2，…)中的最小素数。S.乔拉猜测p(k，l)＝O(k
)，其中ε为任意小的正数。ю.Β.林尼克于1944年首先证明了存在绝对常数с，使得p(k，l)=O(kc)。潘承洞于1957年首先指出с是可以计算的，并定出了с的值。目前最好的结果с≤17是陈景润于1979年得到的。相邻素数之差 设pn是第n个素数，
是相邻的两个素数之差。在黎曼假设下，H.克拉默于1921年证明了
无条件结果 
是赫斯－布朗和H.伊瓦尼克于1979年得到的。另一方面，关于dn的下界，E.邦别里和H.达文波特于1966年证明了：
M.N.赫胥黎于1977年改进为E ≤0.4425。猜测应有E＝0。关于dn还有许多有趣的研究。参考书目
华罗庚著:《指数和的估计及其在数论中的应用》，科学出版社，北京，1963。
K.Prachar，Primzahlverteilung，Springer-Verlag，Berlin，1957.
M.N.Huxley，The Distribution of Prime Number，Clarendon， Oxford，1972.