重心(卷名：力学)
centre of gravity
物体各部分所受重力之合力的作用点。物体的每一微小部分都受地心引力作用（见万有引力），这些引力可近似地看成为相交于地心的汇交力系。由于物体的尺寸远小于地球半径，所以可近似地把作用在一般物体上的引力视为平行力系，物体的总重量就是这些引力的合力。
如果物体的体积和形状都不变，则无论物体对地面处于什么方向，其所受重力总是通过固定在物体上的坐标系的一个确定点，即重心。重心不一定在物体上，例如圆环的重心就不在圆环上，而在它的对称中心上。
重心位置在工程上有重要意义。例如，起重机要正常工作，其重心位置应满足一定条件；舰船的浮升稳定性也与重心的位置有关；高速旋转机械，若其重心不在轴线上，就会引起剧烈的振动等。
重心公式 如将重为W的物体分割为许多微块，微块的重量为dW，在直角坐标系中的坐标为x，y，z，则重心C的坐标可按下式计算：
若物体是均质的，单位体积的重量γ为常数，则W＝γV，dW＝γdV，
这时重心就与形心重合。均质物体重心（或形心）坐标xC、yC、zC的计算公式见表：式中V、A、L分别为物体的体积、面积和长度；dV、dA、dL分别为微块的体积、面积和长度。
形状规则的均质物体，凡具有对称面、对称轴和对称中心的，其重心一定在对称面、对称轴和对称中心上。
计算复杂形状物体的重心位置时，可把它分成若干个简单形状的物体（分体）。设把原物体（组合体）分成n个分体，Wi为第i个分体的重量，xi、yi、zi为第i个分体的重心坐标，W为组合体的总重量。组合体的重心可按下式计算：
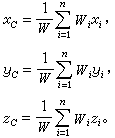
重心位置的测定 一般采用悬挂法和称重法。
①悬挂法 用均质板按一定比例作成模拟的物体(如叶片)截面（图1）。先从叶片上任一点A处悬挂，根据二力平衡条件，重心C处在过悬挂点的铅垂线（图中虚线）上。然后在叶片上另选一个悬挂点B，作第二次悬挂，并过第二个悬挂点画铅垂线。以上两线的交点C即为重心的位置。
②秤重法 先用秤称出物体的重量W，然后将物体的一端支承于固定的支点A，另一端支承于磅秤上（图2）。
量出A、B两点间的水平距l，磅秤上的读数为B点的反力RB，物体的重心位置可由下式求出：
。帕普斯定理 古希腊数学家帕普斯找出了物体重心位置同它旋转后所成回转体的表面积和体积的关系。这种关系后称为帕普斯定理，又称古尔丁定理。内容如下：
第一定理（回转体表面积的计算法） 平面曲线绕平面内同它不相交的轴旋转所成曲面的面积S，等于此曲线的长度l和它的重心(坐标为xC)所画出圆周的长度之乘积，计算公式为：
S=2πxCl。
第二定理（回转体的体积计算法） 平面图形绕其平面内同它不相交的轴线旋转所得的回转体，其体积等于此图形面积S乘以图形面积的重心所画出圆周的长度，计算公式为：
V=2πxCS。