约束优化方法(卷名:数学)
constrained optimization method
寻求具有约束条件的线性或非线性规划问题解的数值算法。假设ƒ(尣),gi(尣)(i=1,2,…,m)是n维欧几里得空间Rn中的实值函数。所谓约束优化问题,是指在约束条件gi(尣)≤0(i=1,2,…,m)之下求一点
 ,使ƒ(尣)≥ƒ(
,使ƒ(尣)≥ƒ( ),点
),点 称为最优解。约束优化问题当ƒ(尣)、gi(尣)(i=1,2,…,m)均为凸函数时称为凸规划。凸函数有很多已知特性,因此凸规划算法的研究进展较快。线性规划是凸规划的最简单的情形,可以用单纯形方法等求解。约束优化问题当ƒ(尣)是二次函数而gi(尣)(i=1,2,…,m)是线性函数时称为二次规划。G.B.丹齐克和P.沃尔夫于1963年将单纯形方法作了修改,用以求解凸二次规划,得到只经过有限次迭代即可达到最优解的算法。
称为最优解。约束优化问题当ƒ(尣)、gi(尣)(i=1,2,…,m)均为凸函数时称为凸规划。凸函数有很多已知特性,因此凸规划算法的研究进展较快。线性规划是凸规划的最简单的情形,可以用单纯形方法等求解。约束优化问题当ƒ(尣)是二次函数而gi(尣)(i=1,2,…,m)是线性函数时称为二次规划。G.B.丹齐克和P.沃尔夫于1963年将单纯形方法作了修改,用以求解凸二次规划,得到只经过有限次迭代即可达到最优解的算法。对于只有等式约束的非线性规划,经典的拉格朗日乘子法指出,在对函数加以一定限制下,最优解可在一组函数方程的解集中去寻求,但是并未指出行之有效的算法。1951年,H.W.库恩和A.W.塔克尔发表“论非线性规划”一文后,随着计算技术的迅速发展,线性约束的非线性规划出现了不少行之有效的算法。在非线性约束规划的研究上,近十几年来也有相当的进展。
可行方向法 根据逐次沿可行方向求可行解点的迭代思想构造一点列{尣k},使其满足某种给定要求的算法称为可行方向法。假设已知可行解为尣(k),若能找到一个向量
 与步长数λk>0,使
与步长数λk>0,使 ,而当0≤λ≤λk时,线段尣(k)+λ
,而当0≤λ≤λk时,线段尣(k)+λ 属于约束集,则
属于约束集,则  称为约束集在尣(k)处的一个可行方向。可行方向法的关键在于适当选取
称为约束集在尣(k)处的一个可行方向。可行方向法的关键在于适当选取 , 点列{尣(k)}符合一般迭代法的要求。对线性约束的情形,当ƒ(尣)为可微凸函数时有三种较为有效的求
, 点列{尣(k)}符合一般迭代法的要求。对线性约束的情形,当ƒ(尣)为可微凸函数时有三种较为有效的求 的算法:G.藻滕代克于1960年提出的可行方向法, 取
的算法:G.藻滕代克于1960年提出的可行方向法, 取 =y(k)- 尣(k),其中y(k)为ƒ(尣)在 尣(k)处的线性近似函数
=y(k)- 尣(k),其中y(k)为ƒ(尣)在 尣(k)处的线性近似函数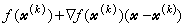 在线性约束下达到最小值的最优解。J.B.罗森于1960年提出的梯度投影法,运用在尣(k)处投影矩阵pk的公式,取最速下降方向-墷ƒ(尣(k))在 尣(k)所处的约束边界面上的投影方向-pk墷ƒ(尣(k))为
在线性约束下达到最小值的最优解。J.B.罗森于1960年提出的梯度投影法,运用在尣(k)处投影矩阵pk的公式,取最速下降方向-墷ƒ(尣(k))在 尣(k)所处的约束边界面上的投影方向-pk墷ƒ(尣(k))为 ,从而避免了每迭代一次就要解一个线性规划的手续。P.沃尔夫于1963年提出的既约梯度法,他应用消去基变量的方法和ƒ(尣)的既约梯度的概念,构造出
,从而避免了每迭代一次就要解一个线性规划的手续。P.沃尔夫于1963年提出的既约梯度法,他应用消去基变量的方法和ƒ(尣)的既约梯度的概念,构造出 。 这三种方法所产生的点列{尣(k)}虽然可以使函数值序列{ƒ(尣(k)}单调下降,但是它却不一定收敛于最优解。因此,后来陆续有不少研究工作,对原有方法进行种种修正,如采取摄动和转轴变换等技巧,而得出具有收敛性的各种新方法。1969年D.戈德福布结合梯度投影法与变尺度法提出了一种可行方向法,对二次凸规划是有限步收敛的。这些方法都可以推广用于处理非线性约束的情形。但是,算法程序都比较复杂。J.阿巴迪和J.卡彭特尔于1969年将既约梯度法加以推广,提出了广义既约梯度法(GRG法)用来求解具有非线性约束的最优化问题。实际计算的效果说明,广义既约梯度法是一种很好的算法。
。 这三种方法所产生的点列{尣(k)}虽然可以使函数值序列{ƒ(尣(k)}单调下降,但是它却不一定收敛于最优解。因此,后来陆续有不少研究工作,对原有方法进行种种修正,如采取摄动和转轴变换等技巧,而得出具有收敛性的各种新方法。1969年D.戈德福布结合梯度投影法与变尺度法提出了一种可行方向法,对二次凸规划是有限步收敛的。这些方法都可以推广用于处理非线性约束的情形。但是,算法程序都比较复杂。J.阿巴迪和J.卡彭特尔于1969年将既约梯度法加以推广,提出了广义既约梯度法(GRG法)用来求解具有非线性约束的最优化问题。实际计算的效果说明,广义既约梯度法是一种很好的算法。上述线性近似型算法的收敛速度,一般都不高于超线性的。对二阶可微的函数ƒ(尣),在尣(k)处若用二次函数
 ·
· 来近似,进而对可微函数ƒ(尣)又用种种变尺度矩阵Hk去代替近似式中的矩阵墷2ƒ(尣(k)),将约束问题的求解化为求一系列二次规划的解,这类方法统称为序贯二次规划法,1963年R.B.威尔森对二阶可微函数ƒ(尣),gi(尣)(i=1,2,…,m)提出将拉格朗日函数
来近似,进而对可微函数ƒ(尣)又用种种变尺度矩阵Hk去代替近似式中的矩阵墷2ƒ(尣(k)),将约束问题的求解化为求一系列二次规划的解,这类方法统称为序贯二次规划法,1963年R.B.威尔森对二阶可微函数ƒ(尣),gi(尣)(i=1,2,…,m)提出将拉格朗日函数
 在已知点(尣(k),u(k))处用二次近似函数来逼近,而对约束仍用线性近似函数逼近,并证明了在最优解附近,点列{尣(k)}是二阶收敛的。若用二次函数
在已知点(尣(k),u(k))处用二次近似函数来逼近,而对约束仍用线性近似函数逼近,并证明了在最优解附近,点列{尣(k)}是二阶收敛的。若用二次函数 在尣(k)处逼近目标函数ƒ(尣),其中Hk是正定函数,同时象无约束最优化方法中的变尺度算法一样,利用计算过程中得到的信息和变尺度公式来更新Hk,这种逐次二次规划算法也称为约束变尺度算法。它是求解带非线性约束的最优化问题的重要方法之一。
在尣(k)处逼近目标函数ƒ(尣),其中Hk是正定函数,同时象无约束最优化方法中的变尺度算法一样,利用计算过程中得到的信息和变尺度公式来更新Hk,这种逐次二次规划算法也称为约束变尺度算法。它是求解带非线性约束的最优化问题的重要方法之一。序贯无约束极小化法 1943年R.库朗对于仅带一个约束等式g(尣)=0的问题,引入参数t>0,研究函数ƒ(尣)+t[g(尣)]2的平稳点尣(t)在t→∞时与原问题的关系。对于具有不等式约束gi(尣)≤0(i=1,2,…,m)的非线性规划问题,则作函数
 ;如果将ƒ(尣)看成“价格”,约束看成某种“规定”,则
;如果将ƒ(尣)看成“价格”,约束看成某种“规定”,则 为当尣违反“规定”时的罚款项,于是p(尣,t)就是应支付的总代价。因此,p(尣,t)被称为罚函数,而t称为罚因子。在适当的假设下,p(尣,t)在对尣不加约束的情形下的最优解尣(t),当t→∞时趋于原问题的最优解。这种方法称为罚函数法。由此就可以用逐渐加大tk的方法来求得原问题近似解尣(tk)。为了克服p(尣,t)的黑塞矩阵在t→∞时容易产生病态的缺点,W.I.赞格威尔于1967年提出精确罚函数E(尣,t),证明了在适当的假设下,存在t0>0,当t≥t0时E(尣,t)的无约束最优解尣(t)就是原问题的最优解。于是把有约束的最优化问题化为一个无约束的最优化问题。但是这种精确罚函数不是可微的,因而不便于利用一般无约束优化方法。M.R.赫斯泰尼斯和M.J.D.鲍威尔结合拉格朗日乘子法和罚函数法的特点,于1969年对约束为等式的情形提出可微的增广拉格朗日函数
为当尣违反“规定”时的罚款项,于是p(尣,t)就是应支付的总代价。因此,p(尣,t)被称为罚函数,而t称为罚因子。在适当的假设下,p(尣,t)在对尣不加约束的情形下的最优解尣(t),当t→∞时趋于原问题的最优解。这种方法称为罚函数法。由此就可以用逐渐加大tk的方法来求得原问题近似解尣(tk)。为了克服p(尣,t)的黑塞矩阵在t→∞时容易产生病态的缺点,W.I.赞格威尔于1967年提出精确罚函数E(尣,t),证明了在适当的假设下,存在t0>0,当t≥t0时E(尣,t)的无约束最优解尣(t)就是原问题的最优解。于是把有约束的最优化问题化为一个无约束的最优化问题。但是这种精确罚函数不是可微的,因而不便于利用一般无约束优化方法。M.R.赫斯泰尼斯和M.J.D.鲍威尔结合拉格朗日乘子法和罚函数法的特点,于1969年对约束为等式的情形提出可微的增广拉格朗日函数 ,并指出在适当的假设下,存在t0>0,对任意取定的t≥t0,在最优乘子
,并指出在适当的假设下,存在t0>0,对任意取定的t≥t0,在最优乘子 处,L(尣,
处,L(尣, ,t)的无约束最优解
,t)的无约束最优解 必为原问题的最优解,还给出了逐步调整u和t的办法。以后陆续有不少工作对一般可微非线性规划,构造了各种不同的可微增广拉格朗日函数,并给出了算法的迭代程序。这类方法统称为广义乘子法。K.R.弗里希鉴于罚函数法产生的点列 {尣(tk)}是从约束集的外部来逼近在约束边界上的最优解,于1955年提出所谓障碍函数
必为原问题的最优解,还给出了逐步调整u和t的办法。以后陆续有不少工作对一般可微非线性规划,构造了各种不同的可微增广拉格朗日函数,并给出了算法的迭代程序。这类方法统称为广义乘子法。K.R.弗里希鉴于罚函数法产生的点列 {尣(tk)}是从约束集的外部来逼近在约束边界上的最优解,于1955年提出所谓障碍函数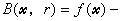
 ,可使B(尣,r)的无约束最优解尣(r)在约束集内达到,而当r→0时,尣(r)趋于原问题的最优解。1961年,C.W.卡罗尔提出了另一种典型的障碍函数
,可使B(尣,r)的无约束最优解尣(r)在约束集内达到,而当r→0时,尣(r)趋于原问题的最优解。1961年,C.W.卡罗尔提出了另一种典型的障碍函数
 。当r→0时,B(尣,r)的黑塞矩阵也可能出现病态现象。
。当r→0时,B(尣,r)的黑塞矩阵也可能出现病态现象。对兼有等式和不等式约束的最优化问题,可结合使用罚函数与障碍函数而构造出混合型函数来求解;对兼有线性和非线性约束的最优化问题,可仅将非线性约束纳入p(尣,t)(或B(尣,r),或L(尣,u,t)),将问题化为在线性约束下p(尣,t)(或B(尣,r),或L(尣,u,t))的极小化问题。
对于不可微的凸规划,近十多年来有人用次梯度或差分等概念来建立算法。设ƒ为Rn中的凸函数,若矢量
 满足
满足 ,则矢量
,则矢量 称为函数ƒ 在点尣0处的一个次梯度。不可微凸规划的最优解在一定条件下满足以次梯度表示的推广的库恩-塔克尔条件(见非线性规划)。函数在一点的次梯度不一定是惟一的。可微函数在一点的梯度若不为零,其负梯度方向必是函数在此点的一个下降方向。然而不可微函数在一点的某些负次梯度可以不是函数的下降方向。这将导致上述可微情况的约束优化算法对于不可微凸规划往往会失败。不可微凸规划的次梯度算法类的基本迭代公式是
称为函数ƒ 在点尣0处的一个次梯度。不可微凸规划的最优解在一定条件下满足以次梯度表示的推广的库恩-塔克尔条件(见非线性规划)。函数在一点的次梯度不一定是惟一的。可微函数在一点的梯度若不为零,其负梯度方向必是函数在此点的一个下降方向。然而不可微函数在一点的某些负次梯度可以不是函数的下降方向。这将导致上述可微情况的约束优化算法对于不可微凸规划往往会失败。不可微凸规划的次梯度算法类的基本迭代公式是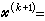
 ,这里tk和
,这里tk和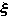 (k)分别是按一定规则选定的步长和点 尣(k)的次梯度(或近似次梯度)。在一些适当的条件下可证明,次梯度算法产生的点列{尣(k)}收敛到问题的最优解。
(k)分别是按一定规则选定的步长和点 尣(k)的次梯度(或近似次梯度)。在一些适当的条件下可证明,次梯度算法产生的点列{尣(k)}收敛到问题的最优解。赞格威尔1969年提出用统一的观点研究算法。他的基本思想是,将算法看成是一个点到集的映像。在一些假设下由上半连续的点到集映像产生的点列 {尣(k)}收敛于最优解。从而统一了不少已有算法的收敛性的研究。这方面的工作还在不断发展。
参考书目
M.阿弗里尔著,李元熹等译:《非线性规划-分析与方法》,上册,上海科学技术出版社,上海,1979。(M.Avriel,Nonlinear Programming-Analysis and Method,Prentice-hall,Englewood Cliffs,New Jersey,1976.)
A.V.Fiacco and G.P.McCormick,Nonlinear Pro-gramming Sequential Unconstrained Minimization Techiques, John Wiley & Sons, New York, 1968.