阶(卷名：自动控制与系统工程)
order
表征线性系统结构的一个主要参数，它的具体含义决定于描述系统的模型形式。对于能控、能观测的系统来说，各种模型形式的阶等于状态空间的维数。设多变量离散时间线性系统(见线性系统)有p个输入u1,u2，…，up和q个输出y1，y2,…，yq,它的系统模型有传递函数阵模型、状态空间模型、传递函数展开式和多项式矩阵模型四种主要形式。
① 传递函数阵模型
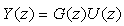
式中
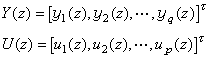Y(z)和U(z)分别是y(t)和u(t)在零初始条件下的Z变换。q×p维矩阵G(z)是系统的传递函数阵,它的元素是z的有理函数。矩阵G(z)的所有元素的最小公分母的次数称为系统的阶。② 状态空间模型
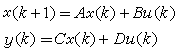式中x(k)是n维状态向量，u(k)是p维输入向量，y(p)是q维输出向量。这时，状态变量的个数,或者说状态空间的维数称为系统的阶。③ 传递函数展开式模型 若将传递函数阵G(z)展开成无穷级数
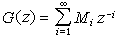则系统完全由矩阵列Mi，i=1,2…所决定。{Mi，i=1,2,…} 称为马尔可夫参数。由马尔可夫参数构成无穷维矩阵H
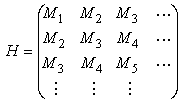称为汉克尔矩阵。矩阵H的秩称为系统的阶。④ 多项式矩阵模型
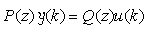式中y(k)是q维输出向量, u(k)是p 维输入向量，P(z)和Q(z)分别是q×q维和q×p维的多项式矩阵,即它们的元素都是z的多项式。z是向前移位算子: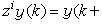
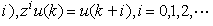。P(z)的阶次称为系统的阶。当p=q=1时,就得到单输入单输出系统的阶。对于连续时间线性系统也有类似的结果,这时只需把Z变换改为拉普拉斯变换，移位算子z改为微分算子D。如果系统是完全能控(见能控性),完全能观测（见能观测性）的,这时(A，B，C)是最小实现,P(z)与Q(z)互质。在上述各种模型下给出的系统的阶的定义是一致的，它们都是状态空间的维数。