质点运动微分方程(卷名：力学)
differential equations of motion of a particle
用牛顿第二定律描述质点运动的微分方程。设质量为m的质点Q，在F1，F2，…， FN诸力的作用下运动。若以a表示质点的加速度，以
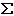F表示诸力的合力（见图），则由牛顿第二定律有：
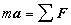， (1)或写成：
，式中r为质点的矢径。这是矢量形式的质点运动微分方程。
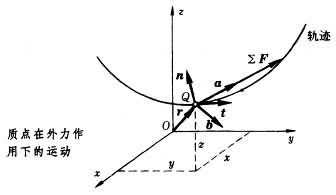
把式(1)在直角坐标轴上投影，得：
(2)这是直角坐标轴投影形式的质点运动微分方程。若把式(1)投影到图中的(t、n、b)自然坐标轴上，则有：
(3)式中ρ是质点在其轨迹上所在点的曲率半径。式(3)是自然坐标轴投影形式的质点运动微分方程。从(3)可以看出，作半径为R的匀速圆周运动的质点，只受向心力作用，其值为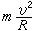
，其中υ为速率。 以上各种形式的质点运动微分方程都建立了质点的运动与作用力之间的关系。知其一就能求出其二，因此，应用它可以解决两类问题：
①第一类质点动力学问题 已知质点的运动规律，求质点上的作用力。设已知质点在直角坐标中的运动方程为：
将其对时间微分两次，应用式(2)可得质点上的作用力的三个分力。②第二类质点动力学问题 已知质点上所受的力，求质点的运动规律，即从质点运动微分方程通过积分求解质点的运动方程。在一般情况下，质点上所受的力既可能是常力，也可能是随时间、速度、位置而变化的变力。因此，∑Fx、∑Fy、∑Fz是t、x、y、z、夶、夻、妰的函数。于是式(2)有以下形式：
这是三个二阶微分方程，积分后将得到包含六个积分常数的解，即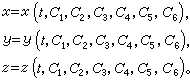
上式中六个积分常数要由质点运动的初始条件来确定。这个初始条件就是质点的初始位置和初始速度。当t=0时，初始位置为
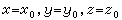;初始速度为υx=夶0，υy=夻0，υz=妰0。在解决具体问题时，必须知道初始条件，才能得到确定的解答。在动力学中还有一些问题是这两类问题的综合。