雅可比矩阵(卷名：数学)
Jacobian matrix
以m个n元函数uj=uj(x1，x2，…，xn)(i=1，2，…，m)的偏导数
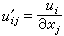(j=1，2，…，n)为元素的矩阵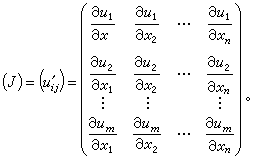
如果把原来的函数组看作由点x=(x1，x2，…，xn)到点u=(u1，u2，…，um)的一个变换T，则在偏导数都连续的前提之下，u随x的变化由相应的微分方程组
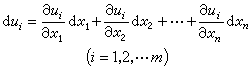来描述。这是一个关于微分的线性方程组，其系数矩阵便是雅可比矩阵(J)，因而可写成矩阵形式
这隐含着(J)具有微分系数的某些性质，类似于一元函数的导数。而在m=n=1的情形，它又恰好是一个一元函数的导数；所以它也是一个一元函数的导数到m个n元函数的一种推广。因此，(J)作为微分系数或导数的推广，有时也被当作变换T的“导数”看待并记为T′(x)=(J)。变换T的进一步的数量描述需要雅可比行列式。