集合(卷名:数学)
set
数学中的基本概念,集合论的主要研究对象。一定范围的、确定的、可区别的事物,当作一个整体来看待,就叫作集合,简称集,其中各事物叫作集合的元素或简称元。如①北京、天津、上海三城市;②全体英文大写字母;③《阿Q正传》中出现的不同汉字;④全体自然数;⑤平面上的所有直线,都是集合的例。但池子中的水,古今著名小说就不算集合,因为不满足确定与可区别的条件。事物m是集合S的元素有时也说成m属于S 或S含有m,记为m∈S。如果集合只含有有限个元素,便称为有穷集合,否则称为无穷集合。在上面的例中,前三个是有穷集合,后两个是无穷集合。
按照集合的定义,当一个集合的所有元素都已知时,这个集合就确定了。这时如果它是有穷集,便可将其元素全部列出,置于括弧之内来表示(什么顺序都无关系)。如①{北京、天津、上海},②{A,B,C,…,Z},对于③虽有困难,但原则上还是办得到的。但是,如果集合是无穷集,那么,上面的方法就行不通了。这时只好利用能够刻画所有元素x的某一性质 P(x)来加以概括。如例 ④中的集合可表示为{x|x 是自然数}。这种表示也适用于有穷集,如{北京、天津、上海}={x|x=北京或x=天津或x =上海}={x|x为中国现有直辖市}。一个集合可以没有任何元素,这种集合只有一个,叫作空集,通常用北欧字母
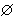 来记它。如果集合B的元素都是A的元素,就称B为A的子集,或A包含B,记为B嶅A 。例如,偶数全体嶅自然数全体。空集
来记它。如果集合B的元素都是A的元素,就称B为A的子集,或A包含B,记为B嶅A 。例如,偶数全体嶅自然数全体。空集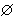 被看作是任何集合的子集。任一集合A都是它自己的子集,即A嶅A 。A的异于自己的子集 B称为 A的真子集,记为B
被看作是任何集合的子集。任一集合A都是它自己的子集,即A嶅A 。A的异于自己的子集 B称为 A的真子集,记为B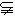 A 。两集合的相等(即含有同样的元素)可用包含关系来表达:A=B当且仅当 A嶅B且B嶅A 。包含关系还具备传递性:即由 A嶅B,B嶅C可得A嶅C。要注意的是,属于关系∈与包含关系嶅是有区别的:∈是元素对集合的关系,而嶅是集合对集合的关系。可以有
A 。两集合的相等(即含有同样的元素)可用包含关系来表达:A=B当且仅当 A嶅B且B嶅A 。包含关系还具备传递性:即由 A嶅B,B嶅C可得A嶅C。要注意的是,属于关系∈与包含关系嶅是有区别的:∈是元素对集合的关系,而嶅是集合对集合的关系。可以有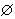 嶅
嶅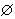 ,但
,但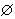 ∈
∈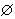 不成立。
不成立。从任意两个集合A与B可以得到一些新的集合。以属于A或属于B的元素为元素的集合称为A与B的并(集),记为A∪B(A与B中的相同元素在并集中出现一次)。以属于A且属于B的元素为元素的集合称为A与B的交(集),记为A∩B。以属于A而不属于B 的元素为元素的集合称为A与B的差(集),记为A\\B;特别,当B嶅A时,可记为CAB,称为B关于A的补(集)。例如A={0,1,3},B={0,3,5,10},则A∪B={0,1,3,5,10},A∩B={0,3},A\\B={1}。并与交的运算分别服从交换律,结合律且共同服从分配律,即对任意的A,B,C,有
A∪B=B∪A,(A∪B)∪C=A∪(B∪C),
A∩B=B∩A,(A∩B)∩C=A∩(B∩C),
A∩(B∪C)=(A∩B)∪(A∩C),
A∪(B∩C)=(A∪B)∩(A∪C)。它们与差运算一起服从德·摩根定律:
S\\(A∪B)=(S\\A)∩(S\\B),
S\\(A∩B)=(S\\A)∪(S\\B)。这里S为任一集合,特别当S包含A与B时,有
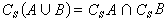 ,
,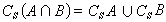 。一个集合也可以以其他集合为元素。这就是所谓集合的集合,如上面例⑤就是一个集合的集合,如果把直线看做是点的集合的话。一个集合 A的所有子集组成的集合是一个很重要的集合的集合,称为A的幂集,记为P(A)。例如,当A={1,2,3}时,P(A)={
。一个集合也可以以其他集合为元素。这就是所谓集合的集合,如上面例⑤就是一个集合的集合,如果把直线看做是点的集合的话。一个集合 A的所有子集组成的集合是一个很重要的集合的集合,称为A的幂集,记为P(A)。例如,当A={1,2,3}时,P(A)={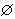 ,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}}。集合的集合是所谓集合族的特殊情形。一般而论,如果对于某一集合I(≠
,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}}。集合的集合是所谓集合族的特殊情形。一般而论,如果对于某一集合I(≠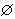 )的每一个元素I∈I,都指定有一个确定的集合Ai,那么,这些Ai的全体就称为一个集合族,记为{Ai,i∈I}。例如,当I=N即自然数全体时,{Ai,I∈N}就是集合序列:A1,A2,A3,…。集合族的成员一般允许有重复,如果没有重复时,它就是一个集合的集合。对于集合族{Ai,I∈I},可定义它的并为{x|对某I∈I,x∈Ai},记为
)的每一个元素I∈I,都指定有一个确定的集合Ai,那么,这些Ai的全体就称为一个集合族,记为{Ai,i∈I}。例如,当I=N即自然数全体时,{Ai,I∈N}就是集合序列:A1,A2,A3,…。集合族的成员一般允许有重复,如果没有重复时,它就是一个集合的集合。对于集合族{Ai,I∈I},可定义它的并为{x|对某I∈I,x∈Ai},记为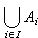 。仿此,可定义它的交为{x|对一切I∈I,x∈Ai},记为
。仿此,可定义它的交为{x|对一切I∈I,x∈Ai},记为 。特别当I={1,2,…,n}时,通常将并写成
。特别当I={1,2,…,n}时,通常将并写成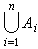 ,将交写成
,将交写成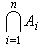 ;当n=2时,就是上面的A1∪A2和A1∩A2。当I=N时,通常将并写成
;当n=2时,就是上面的A1∪A2和A1∩A2。当I=N时,通常将并写成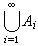 ,将交写成
,将交写成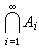 。两个对象α,b按一定次序(譬如α在前,b在后)排列起来,称为一个序对,记为<α,b>,α称为它的第一坐标,b称为第二坐标。两个序对<α,b>,<α′,b′>当且仅当 α= α′,b=b′即各坐标分别相等时,规定它们是相等的。因此,除非α=b,<α,b>≠<b, α>。也可直接定义<α,b>为{{α},{α,b}},虽不大自然,却很精确。同样可定义一般的有序n组。设A,B为两个集合,从A,B中各取一个元素α,b所作序对<α,b>的全体组成一个集合,即{<α,b>|α∈A且b∈B},它称为A与B(按这次序)的直积或笛卡儿积,记为A×B。直积概念也可从两个因子推广到n个因子,A1×A2×…×An,记为
。两个对象α,b按一定次序(譬如α在前,b在后)排列起来,称为一个序对,记为<α,b>,α称为它的第一坐标,b称为第二坐标。两个序对<α,b>,<α′,b′>当且仅当 α= α′,b=b′即各坐标分别相等时,规定它们是相等的。因此,除非α=b,<α,b>≠<b, α>。也可直接定义<α,b>为{{α},{α,b}},虽不大自然,却很精确。同样可定义一般的有序n组。设A,B为两个集合,从A,B中各取一个元素α,b所作序对<α,b>的全体组成一个集合,即{<α,b>|α∈A且b∈B},它称为A与B(按这次序)的直积或笛卡儿积,记为A×B。直积概念也可从两个因子推广到n个因子,A1×A2×…×An,记为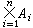 ,特别当各Ai均等于A时,称为A的n次直幂,记为An,它相当于所有从{0,1,…,n-1}到A的映射全体组成的集。推而广之,所有从B到A的映射全体组成的集可以记为A
,特别当各Ai均等于A时,称为A的n次直幂,记为An,它相当于所有从{0,1,…,n-1}到A的映射全体组成的集。推而广之,所有从B到A的映射全体组成的集可以记为A 。
。