集团展开(卷名：物理学)
cluster expansion
即通过计算配分函数求得级数形式的物态方程，用以描述实际气体的一个常用的有效方法。这种方法是由H.D.乌泽耳以及J.E.迈尔夫妇等人建立和发展起来的，它适用于温度不太低或密度不太高的气体系统。
运用集团展开的方法，可把实际气体的压强p展成密度ρ的幂级数，而幂级数的各个系数用位形空间中的某些积分来表示。
对于粒子间存在相互作用的系统，使用统计方法时最主要的是要计算巨配分函数
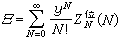中的位形积分
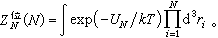式中
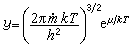称为经典易逸度，μ是化学势，k和 h分别是玻耳兹曼常数和普朗克常数，T是热力学温度，UN是N个粒子系统的总势能，
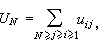uij是两个粒子之间的相互作用势能。当粒子之间的距离rij →∞时，uij比
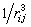更快地趋于零，而exp(-uij/kT)则变为1。引入迈尔函数fij：
fij＝f(rij)=exp(-uij/kT)-1，可得：
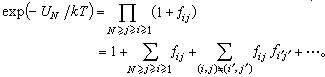式中包含了很多项，非常繁复，采用图示法讨论较方便：用圆圈中加数字表示某个粒子，无直线联结的就表示数值1，两圆圈连一直线就表示fij因子，与若干直线对应的是若干个因子fij的积。例如当N=3时，exp(-U3/kT)的图示法是
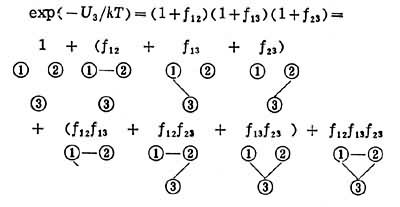对于N个粒子，把相应的乘积开展，会有许多项。在N个点之间不论用直线或不用直线相联，都称为一个图形，exp(-UN/kT)的展开式中的每一项都可以画出相应的图形。在图形中任一点同其他点有直接或间接直线相联的就为一集团。这样，每个集团对应于因子积
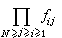。每个图形由一个集团或若干个集团组成。exp(-UN/kT)展开式中的每一项都对应于把代表N个粒子的N个点以一定方式分组为若干个集团，若在某种分组中，一个点的集团有m1个，二个点的集团有m2个，…l个点的集团有ml个等等，所有这些ml应满足关系
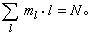于是，exp(-UN/kT)是同所有满足此式的分组所对应的图形的和。由于各个 l个点的集团中联线不同，因此每个exp(-Ul/kT)中还包含若干项，它可表示为
同时每个exp(-Ul/kT)对Л个粒子坐标的积分是相同的。由于每一Л点的集团中的Л个粒子可从N个粒子中任选，排列组合满足上式的固定一套{ml}分组的分法共有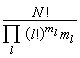
种。因此，若定义集团积分bl为
则可求在固定一套分组{ml}下，对位形积分的贡献：
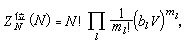而得到：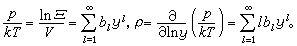
可见，在研究非理想气体时，可把p/kT按粒子数密度ρ展成级数，其中各个系数称为各级维里系数。这个方法同样可以运用于粒子间相互作用多于两体的情形。此外，B.卡恩和G.E.乌伦贝克建立了量子统计力学的集团展开法。
参考书目
J.梅逸、M.G.梅逸著，陈成琳等译：《统计力学》，高等教育出版社，北京，1957。(J.Mayer and M.G.Mayer，Statistical Mechanics，Wiley， New York，1946.)
Kerson Huang，Statistical Mechanics， John Wiley & Sons，New York， London，1963.