维纳－霍普夫方程(卷名：数学)
Wiener-Hopf equation
一类给定在半无穷区间上的带差核的奇异积分方程，其一般形式为
(1)式中μ为常数;k(x)(-∞<x<+∞)和ƒ(x)(0≤x<+∞)为已知函数；φ(x)(0<x<+∞)为未知函数。方程(1)的研究开始于20世纪20年代初，它早期的著名例子是辐射传输理论中的米尔恩方程，后来因1931年N.维纳和E.霍普夫给出其求解方法而得名。20世纪40年代以后，这一方程的理论在解析函数边值问题、调和分析和算子理论的基础上得到了系统的发展，其应用也从辐射问题扩展到许多其他领域，例如中子迁移、电磁波衍射、控制论、多体问题以及人口理论等。
维纳-霍普夫方法 又称因子分解法，是N.维纳和E.霍普夫为求解方程(1)而提出的，已成为研究各种数学物理问题的一种常用方法。其基本思想是通过积分变换将原方程化为一个泛函方程，然后再用函数因子分解的方法来求解。下面以方程(1)的求解为例来加以说明。 在x<0处，令φ(x)=ƒ(x)=0，首先将方程(1)开拓到整个实轴，即
式中
若（2）中诸函数满足适当的条件，例如，存在h>0使得k(x)e
，φ(x)ehx和ƒ(x)ehx属于L1(-∞，+∞)，则借助于傅里叶变换由(2)可得
这里和下文大写字母均表示相应函数的傅里叶变换，而大写字母的下标+和－则分别表示该函数在半平面τ>－h和τ<h内解析。在许多情况下，对(3)可求出解的表达式。求解的关键在于将H(λ)=μ-K(λ)因子分解。一个常用的分解定理是，设H(λ)在｜λ｜<h内解析、无零点且一致地有
则存在分解
式中H+(λ)和H-(λ)可由H(λ)求出，它们在相应半平面内无零点。由于在所述条件下，F+(λ)/H-(λ)在｜τ｜<h内解析，
由柯西积分公式知，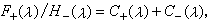
这里C+(λ)和C-(λ)可用
来表示，因而由(3)得到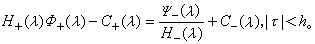
由此利用解析开拓和广义刘维尔定理求出φ+(λ)和ψ-(λ)（准确到相差一个整函数），然后再对φ+(λ)进行傅里叶逆变换即可求得方程(1)的解φ(x)。当仅假定k(λ)∈L1(-∞，+∞)和μ-K(σ)≠0(-∞≤σ≤+∞)时，μ-K(σ)也有类似分解，这时需要用到调和分析理论中的维纳－莱维定理。由此应用巴拿赫空间中的算子理论，还可在一般函数空间，例如
有界可测函数空间和有界连续函数空间中对方程 (1)进行求解。主要结果 用E记上述函数空间。方程(1)的一个重要特点是其中积分仅是相应函数空间中的有界算子，而不是全连续算子，因此它和弗雷德霍姆积分方程在性质上有着本质的不同。这主要表现在:①齐次方程(1)和它的共轭方程线性无关解的个数一般不相等，它们的差等于
整数v(μ)称为方程(1)的指标；②方程(1)的谱点一般为连续统，其中复平面闭曲线μ=K(σ)(-∞≤σ≤+∞)上的点为本质谱，亦即对于全连续算子微扰不变的谱，而使得v(μ)>0的点μ为方程(1)的点谱。函数 μ-K(σ)称为方程(1)的符号。当符号无零点时，方程（1）称为正常的，否则称为例外的。对于正常方程，已经有了较系统的结果，其中主要有：① 设k（x）∈L1(-∞，+∞)，则方程(1)在E中满足诺特定理(见奇异积分方程)的充分必要条件为μ-K(λ)≠0(-∞≤σ≤+∞)，故正常方程有时也称为诺特型方程；②当v(μ)>0时，齐次方程（1）在E中有v(μ)个线性无关解，v(μ)≤0时无非零解；③当v(μ)>0时，非齐次方程(1)在E中有v(μ)个线性无关解，v(μ)=0时，有惟一解，v(μ)<0时，无解或有惟一解，有解的充分必要条件是其右端满足条件
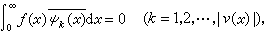式中ψk(x)是方程(1)的共轭方程
的线性无关解。至于例外方程，也有不少结果，但尚无系统理论。以上结果在作相应修改后，对于对偶积分方程、方程 (1)的离散形式特普利茨方程以及有关方程组也都同样成立。
参考书目
S.Prssdorf，Some Classes of Singular Equations，North-Holland，Amsterdam，1978.
B.Noble，Method based on the Wiener-Hopf Technique for the Solution of partial Differential Equations， Pergamon Press， London， 1958.