解析函数项级数(卷名:数学)
series of analytic functions
由解析函数组成的级数。在实分析中,可导函数的一致收敛级数不一定可导。例如由外尔斯特拉斯定理知道,在[α,b]上连续的任何函数可表示为一致收敛的多项式级数。在复分析中有不同的结果:一致收敛的解析函数项级数是解析函数。
设ƒn(z)(n=1,2,…)是在区域D内连续的函数。如果对任何紧集K嶅D以及任何ε>0,存在着正整数N=N(K,ε),使得对n≥N及任何z∈K,
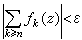 ,则称级数
,则称级数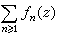 (简写为
(简写为 )在D内任何紧集上一致收敛。如果对任何紧集K嶅D,级数
)在D内任何紧集上一致收敛。如果对任何紧集K嶅D,级数 收敛,则称
收敛,则称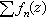 在D内任何紧集上正规收敛。正规收敛性在应用中是常见的;显然,如果
在D内任何紧集上正规收敛。正规收敛性在应用中是常见的;显然,如果 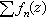 在D内任何紧集上正规收敛,那么它在这种集上一致收敛。
在D内任何紧集上正规收敛,那么它在这种集上一致收敛。应用柯西公式(见柯西积分定理),K.外尔斯特拉斯证明了下列定理:设ƒn(z)(n=1,2,…)在区域 D 内解析,如果
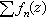 在D内任何紧集上一致收敛,那么它的和ƒ(z)在D内解析,而且在D内,
在D内任何紧集上一致收敛,那么它的和ƒ(z)在D内解析,而且在D内, ,此式右边的级数在D内任何紧集上一致收敛。如果
,此式右边的级数在D内任何紧集上一致收敛。如果 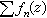 在D内任何紧集上正规收敛,那么级数
在D内任何紧集上正规收敛,那么级数 在D内任何紧集上也正规收敛。
在D内任何紧集上也正规收敛。形如
 (简记为
(简记为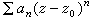 ,式中αn和z0为复数)的级数是一种特殊的解析函数项级数,称为幂级数。
,式中αn和z0为复数)的级数是一种特殊的解析函数项级数,称为幂级数。对于这种级数有下列阿贝尔引理:设
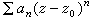 在z1≠z0收敛。则对满足
在z1≠z0收敛。则对满足 的任何z,级数绝对收敛。
的任何z,级数绝对收敛。由这引理出发,可以证明任何幂级数
 属于下列三种情况之一。
属于下列三种情况之一。① 存在着有限正数R;级数在圆盘|z-z0|<R内绝对收敛而且在这圆盘内任何紧集上正规收敛;当|z-z0|>R时,级数发散。这时R称为级数的收敛半径,|z-z0|<R称为收敛圆盘,|z-z0|=R 称为收敛圆周。
② 对任何z≠z0,级数发散;这时称级数的收敛半径为0。
③ 对任何z,级数收敛,从而在任何紧集上正规收敛;这时称级数的收敛半径为+∞。
由外尔斯特拉斯定理,在第一种情况下,幂级数在收敛圆盘内解析,并且可逐项求导数;在第三种情况下,幂级数表示一整函数(即在整个有限复平面解析的函数),并且可在有限复平面内逐项求导数。
在第一种情况下,幂级数在其收敛圆上的点可能收敛,也可能发散。例如
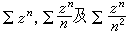 的收敛半径都是1,而在收敛圆周上,第三个级数处处收敛;第一个级数处处发散;第二个级数在-1收敛,在1发散(可证明它在收敛圆周上除去1外处处收敛)。对于在圆周上某些点收敛的幂级数,有下列阿贝尔-施托尔茨定理:设幂级数
的收敛半径都是1,而在收敛圆周上,第三个级数处处收敛;第一个级数处处发散;第二个级数在-1收敛,在1发散(可证明它在收敛圆周上除去1外处处收敛)。对于在圆周上某些点收敛的幂级数,有下列阿贝尔-施托尔茨定理:设幂级数 有收敛半径R(0<R<+∞),并且它在收敛圆周上一点z*收敛。作以z*为顶点、以z0及z*的联线为平分角线,并且角度小于π的角。那么当z在收敛圆盘内且在这角域内趋近于z*时,有
有收敛半径R(0<R<+∞),并且它在收敛圆周上一点z*收敛。作以z*为顶点、以z0及z*的联线为平分角线,并且角度小于π的角。那么当z在收敛圆盘内且在这角域内趋近于z*时,有 。
。幂级数
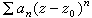 的收敛半径R可以用下列柯西-阿达马公式求出:
的收敛半径R可以用下列柯西-阿达马公式求出: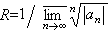 ;当上式右边中分子为+∞时,R=0;当它为0时,R=+∞。
;当上式右边中分子为+∞时,R=0;当它为0时,R=+∞。