网络流(卷名：数学)
network flows
图论中一种理论和方法，研究网络上的一类最优化问题。T.E.哈里斯于1955年研究铁路网的最大通过能力时首先提出，在一个给定的网络上寻求某两点间的最大运输量问题。1956年，L.R.福特和D.R.富尔克森给出了算法，从而建立了网络流理论。
在网络流问题中，网络是由一个有向图G ＝(V，E)和一个定义在弧集E上的已知非负函数с所组成，其中点集V中有两个指定的点υs和υt，分别称为发点和收点，而V中其他的点都称为中间点；с称为网络的容量函数。用сij表示函数с在弧e＝(υi，υj)上的函数值，并称之为弧(υi，υj)的容量。
设ƒ是定义在集合E上的非负函数。用ƒij表示ƒ在弧e=(υi，υj)上的函数值，并称为在弧e上从υi到υj的流量。若函数ƒ满足以下两个条件，则称函数ƒ为网络上的流，简称网络流：①在每一条弧上，流量ƒij不超过容量сij，即0≤ƒij≤сij；②在任何一个中间点υj上，从υi流出的总流量等于流入υi的总流量，即
，式中
是对所有以υi为起点的弧求和，
是对所有以υi为终点的弧求和。条件②称为流的平衡条件。对任意给定的流ƒ，易见，发点的净出量等于收点的净收量，即
。净出量是指从υs流出的总流量减去流入υs的总流量的差；净收量是指从υt流入的总流量减去从υt流出的总流量的差。以υ(ƒ)表示υs的净出量或υt的净收量，并称为ƒ(在网络上)的流量。如图1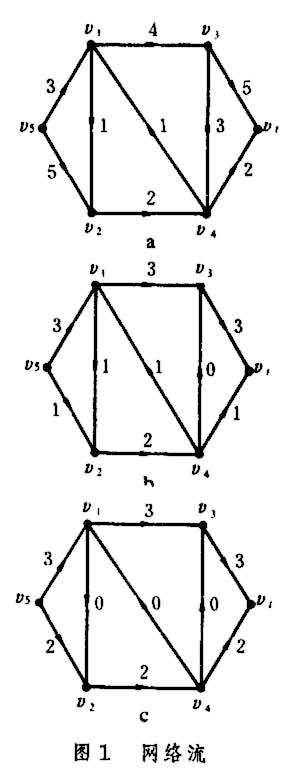
中的a表示一个网络，箭头表示弧的方向，弧上的数表示容量。b、c表示网络a上的两个流，弧上的数字表示该弧的流量。b的流量为4，c的流量为5。由网络中的点组成的序列
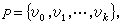若对每一对相继点υi、υi+1或者(υi，υi+1)或者(υi+1，υi)是网络中的弧，则称p是一条连结υ0到υk的链。设p是一条连接υs到υt的链，从υs出发，沿p走到υt时，则链p中与走向有相同方向的弧称为前向弧；有相反方向的称为后向弧。如果对于给定的流ƒ，它在p 的每条前向弧上的流量都小于容量，在每条后向弧上的流量都大于零，则称链 p是关于流ƒ的一个增广链。例如，在图1b中，p＝{υs，υ2，υ1，υ4，υt}是一个增广链。(υs，υ2)、(υ4，υt)是前向弧，其上的流量都小于容量；(υ1，υ2)，(υ4，υ1)是后向弧，其上的流量都大于零。如果在此增广链的前向弧上，流量都增加1，后向弧上流量都减少1，就可从b变到c，从而使流量从4增加到5。在网络上寻求一个使流量 υ(ƒ)达到最大的流ƒ，称之为网络最大流问题。它是网络流理论中的一个主要研究课题，已获得一些重要结果：①流ƒ是最大流的充分必要条件是，不存在关于ƒ的增广链。从而将寻求最大流问题化为判断有无增广链问题。易见，图1中的b不是最大流。福特和富尔克森提出了一种标号法，即对网络上的点给以标号，从υs出发沿网络上的弧向υt探寻增广链的方法。②若各弧上的容量都是正整数，则必存在各弧上的流量都是整数的最大流。③设x是含有υs而不含υt的点集，(X，塣)表示起点在x中而终点不在x中的弧的集合，并称为分离υs和υt的截集，简称截集。网络中去掉一个截集后，就没有从υs到υt的定向链。(X，塣)中所有弧的容量之和，称为这个截集的截量，记作с(X，塣)。使截量最小的截集称为最小截集。网络流理论中有一个基本的对偶定理:最大流的流量等于最小截集的截量。图1的c是一个流量达到最大的流（流量为5），截集{(υs，υ1)，(υ2，υ4)}是一个最小截集（截量为5），这里x＝{υs，υ2}。
最小费用流问题是常见的一类重要的网络流问题。设在网络的每条弧(υi，υj)上，除сij外，还赋予一个数值αij，求出一个流ƒ，使其流量为给定的υ*，而且
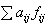取最小值。这里∑是对所有的弧求和，αij可理解为从υi沿弧（υi，υj）运输单位物资到υj的费用，
是总的运输费用。这类问题的解法，一种是从一个流量为υ1(υ1<υ*)的最小费用流ƒ1出发寻求关于流ƒ1的增广链M，使得沿M可以把ƒ1调整为流量是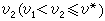
的最小费用流，反复进行，直到得出流量为υ*的流ƒ，或者判明网络中不存在流量为υ*的流。另一种解法是，从流量为υ*的流出发，在不改变流量的情况下，逐步调整，使总费用减少到不能再减少为止。1961年，富尔克森还提出一个求解更一般的最小费用流问题的方法。80年代，一些学者提出了更有效的最小费用流算法。作为网络最大流问题的推广，弧上流量有非零下界的网络流、动态流、带增益的流、多种物资流、网络流的分析和合成等问题，都有了一系列的研究结果。在网络最大流的算法方面也取得了很大的改进。网络流理论已经成为解决许多组合问题的有力工具。组合数学中的一个著名问题，即不同代表系问题：有n个人自由组成m个不同的社会团体，每个人可以同时自由参加几个团体，如何选出m个不同的人，使其分别成为m个团体的代表。这个问题就可用网络流方法解决。例如，设有5个人:｛1，2，3，4，5｝，4个团体：A =｛2，4，5｝，B =｛1，5｝，C =｛3，4｝，D =｛3，4｝，可通过求解图2
的网络最大流得到解答，图2中，未标明容量的弧上，其容量是+∞。｛5，1，3，4｝就可分别成为4个团体的代表。利用网络流的对偶定理，还可证明，霍尔定理:存在各团体的不同代表的充分必要条件是，任何k个团体的成员合在一起的总人数不少于k(1≤k≤n)。在分析交通运输、工程进度以及生产任务时，也往往应用网络流中最小截集的概念来找出薄弱环节。参考书目
L.R.Ford and D.R.Fulkerson，Flows in Networks，Princeton Univ. Press， Princeton.1962.
J.C.Hu，Integer Programming and Network Flows，Addison-Wesley， London，1969.