可遗坐标(卷名：力学)
ignorable coordinates
又称循环坐标，是在拉格朗日函数L中不出现或在哈密顿函数 H中不出现的广义坐标。例如在有心力作用下的质点运动，用球坐标(r，嗞，θ)表达的拉格朗日函数为：
，式中T为质点的动能；V为势函数;m为质点的质量；f(r)为有心力。上式中不出现广义坐标嗞，因而嗞是这个系统的一个可遗坐标。如果一系统有某个可遗坐标qi，则有：
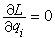。此时由系统的拉格朗日方程得到：
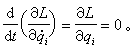因此，该系统有经典的守恒律：与可遗坐标qi相应的广义动量守恒，即
。这是系统拉格朗日方程的一个第一积分，称为循环积分。1876年E.J.劳思应用循环积分，研究出将拉格朗日方程降阶的方法。N个自由度的完整系统，如果有s个可遗坐标，则原2N 阶的微分方程可降低为2(N-s)阶，而仍保持拉格朗日的形式。对于哈密顿正则系统，如果qi是可遗坐标，根据正则方程，得到与qi对应的广义动量pi为常数。利用正则变换可把哈密顿系统尽可能多的广义坐标变换成可遗坐标。对于这样的坐标，哈密顿－雅可比方程的全积分的形式比较简单，其中包含着可遗坐标的一次式。如果选择正则变换，使变换后的哈密顿函数恒等于零，则变换后的全部广义坐标都是可遗坐标，此时系统极易求解。按这种考虑所得到的方法就是哈密顿-雅可比方法。
参考书目
E. T. Whittaker， A Treatise on the Analytical Dynamicsof Particles and Rigid Bodies， 4th ed.， Cambridge Univ.Press，Cambridge，1952.
W.M.Smart， Celestial Mechanics， John Wiley ＆ Sons，Glasgow，1953.