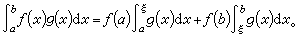中值定理(卷名：数学)
mean value theorem
关于存在某种性质的中间值的定理。例如，一个区间上的连续函数必定达到它在该区间的任何两个函数值之间的每一个中间值。这一事实常称为连续函数的“介值定理”。而关于导数的介值定理又指出，如果函数本身是某个连续函数的导函数，那么即使它不连续，也具有这种取到中间值的性质。
微分学的基本定理都是以中值定理的形式出现的。其中最重要的是拉格朗日定理，它断言，可微函数y=ƒ(x)的平均变化率，必定等于变化区间的某个中间点处的瞬时变化率：
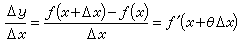或
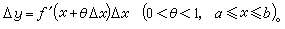
积分学的第一中值定理 连续函数ƒ(x)在区间[α，b]上的积分平均等于它的某个中间值：
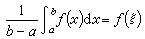或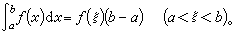
这相当于拉格朗日定理运用于原函数 
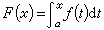在点x＝α处的变化量Δx＝b-α。积分学第二中值定理 对于一个单调函数ƒ(x)与一个可积函数g(x)的乘积在区间［α，b］上的积分，必定存在区间上的一个中间点ξ，使得
