初等常微分方程(卷名：数学)
elementary ordinary differential equation
能用微积分的方法求出其通解或通积分的常微分方程。常微分方程的通解，粗略地说就是：①它把未知函数y表示为自变量x的显函数的形式y=φ(x)，此函数满足该微分方程。②在此表达式中含有一些任意常数，其个数恰等于方程的阶数。当这些常数任意变动时即能得到方程的所有解，除了少数解是例外。③表达式适用于全空间，或至少不是局部的而是大范围的。如果在这定义中不要求①成立，即在所得的表达式中未知函数可能是自变量的隐函数形式φ(x，y)=0，则称此表达式为通积分。通解（或通积分）的严格定义，实际上就是进一步把条件②的后半部作严格的叙述，即要求：对于该表达式所适用的区域中任意给定的初始条件，必能找到任意常数的一组确定的值，使得这组值所对应的解（或积分）能够满足这个初始条件。
出现于方程中的变量x、y可以是实变量，也可以是复变量。一个解y＝φ(x)或积分φ(x，y)=0在(x，y)空间中的轨迹称为方程的积分曲线。当（x，y）为实数时，积分曲线就是（x，y）平面上的曲线。当（x，y）为复数（x=x1+ix2，y=y1+iy2）时，积分曲线是四维实空间（x1，x2，y1，y2）中的二维曲面。通解或通积分的轨迹称为积分曲线族。要求一个解或积分满足已给的初始条件，就是要求由它所确定的积分曲线通过预先给定的一点。
下面根据方程形式的不同，或阶数与个数的不同，分别作简要的介绍：
可分离变量的方程 形如
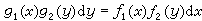(1)的一阶方程称为可分离变量的方程，当 ƒ2(y)g1(x)≠0时，(1)可化为变量已分离的方程
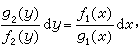两边求积分，即得通积分
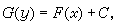(2)式中C为任意常数。如能由(2)解出
， (3)则称之为(1)的通解。(2)或 (3)满足上述对通解或通积分要求。除此以外，还必须再补上使ƒ2(y)=0的一个或多个的常数解y呏yi，以及使g1(x)=0的常数解x呏xj，这些常数解有时能由(2)中令C=0 或1/C=0得到，有时则不能。例如，在用分离变量法求解方程
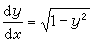时丢掉的解y=±1不能包含在通解 y=sin(x+C)之中。这一类丢掉的解往往是奇解。所谓奇解就是在其上处处破坏初值问题惟一性的解（见常微分方程初值问题）。有些看上去是不能分离变量的方程，通过变量代换可以化为可分离变量的方程来求解。最常遇到的是齐次常微分方程
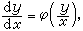(4)它可借代换y=ux而化为
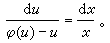这里应注意，一般讲，x=0并非(4)的解。还有一些方程，例如，方程
经代换y=x+u，方程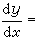
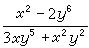经两次代换y3=v及v=ux，均可化为可分离变量的方程。不过用这种方法有时并非易事，也并不一定都能办到。一阶线性方程 形如
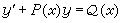(5)的方程称为一阶线性方程，其中P(x)、Q(x)为已知函数。在分离变量法中，x、y被平等地看待，而方程(5)仅当把x看成自变量、y看成未知函数时它才称为线性方程，理由是此方程对于y与y′的总体来说是线性的。称
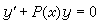(6)为对应的齐次线性方程，它有通解
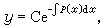(7)式中C 为任意常数。又(6)的满足初始条件y(x0)=y0的特解是
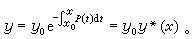(8)对于(5)，可以求它的形如(7)的通解
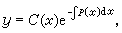(9)但其中C(x)是x的待定的函数。(9)式实际上也是一种变量代换。由此即可求出C(x)，从而得到(5)的通解为
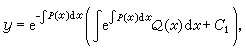(10)式中C1为任意常数。又(5)的满足初值条件y(x0)=y0的特解是
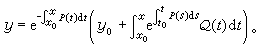(11)以上这种解法称为常数变易法，它同样适用于线性方程组和线性高阶方程。即使对无法求出通解的非线性方程，常数变易公式（类似于(11)式）在理论研究上也是十分有用的。有些微分方程可以通过变量代换而化为一阶线性方程。最常见的是伯努利方程
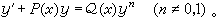(12)所用的变量代换是z=y
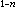。又如对方程 
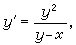可改用x为未知函数、y为自变量而化为 
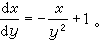又如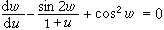
可借变量代换w＝arctan v而化为线性方程，等等。黎卡提方程及其他 在常微分方程的发展史上，黎卡提方程
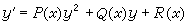(13)有着特殊的重要性。J.F.黎卡提本人研究了(13)的特例
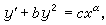(14)证明若α=4k/(1±2k)，(k=0，1，2，…)，则(13)总可通过变量代换而化为可分离变量的方程。方程(13)还有一些其他的可积类型。但是早在1841年J.刘维尔就证明了：当α≠4k/(1±2k)，(14)不能用初等积分法求有限形式的通解，因此，对于一般的(13)，不能用有限次的初等运算求其通解。如果已知(13)的一个特解y1(x)，则借代换y=y1(x)+z可以化(13)为伯努利方程，由此可导出(13)的通解是任意常数的分式线性函数。又若已知(13)的三个特解y1，y2，y3，则通解可由
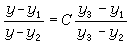给出；从而(13)的任意四个特解的交比恒等于常数。复变量的黎卡提方程在常微分方程解析理论中也有它的重要性，因为它是只可能有动极点而无动支点的方程，此外，它还和微分几何学与复变函数论中的一些重要问题有密切关系。
熟知的可积类型还有：①雅可比方程
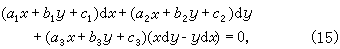它至少有一直线解u1x+u2y+u3=0，而经变量代换
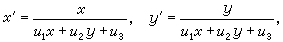则可化为x′，y′的齐次方程。②达布方程
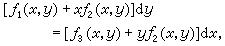(16)式中ƒi(x，y)都是x、y的多项式，其最高次数为m。当有
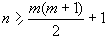个特解为已知时，它是可积分的。③第一类阿贝尔方程
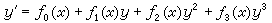和第二类阿贝尔方程
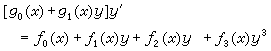它们也有不少情况是可积的。E.卡姆克在他的《微分方程──解法和解》（第 1卷中译本名为《常微分方程手册》，1977）一书中列举了这些情况。秦元勋指出，其中有一半以上的可积一阶方程其通积分都具有（通常称为达布积分）
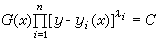(17)的第一类显易解结构及形如
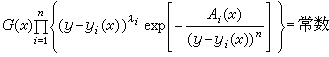的第二类显易解结构。恰当方程与积分因子 满足条件
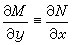(18)的微分方程
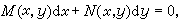(19) (19)称为恰当（微分）方程或全微分方程。(19)式左边可写为dU(x，y)的形式， U(x，y)可借沿特殊道路的线积分求出，而(19)的通积分是U(x，y)=C。但若M、N 的偏导数有不连续点时，则U(x，y)可能是多值函数。当条件(18)不满足时，如果能找到函数 μ(x，y) 使
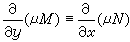或即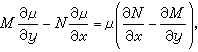
(20)则方程μMdx＋μNdy =0便成为恰当方程。称 μ(x，y)为(19)的积分因子。积分因子有无数个之多，当已知一个积分因子μ时，其他的积分因子便都可写成 μφ(U)的形式，因此μ1(x，y)/μ2(x，y)=C也是(19)的通积分。(20)是关于μ(x，y)的一阶线性偏微分方程，求它的通解比求(19)的通解困难。但当M、N满足一定的条件时可以只求(20)的一个一元函数特解。例如，若
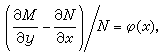(21)即(21)式左边的表达式与y无关，则这时(20)有解
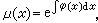它就是(19)在条件(21)之下的积分因子。仿此，可以得出(19)有形如 μ(y)，
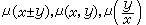等形状的积分因子时所应满足的条件。易见方程(1)实际上是借积分因子
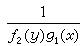而被化为恰当方程(2)，方程(5)满足条件(21)，故有积分因子
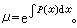又当(19)为齐次方程且xM+yN扝0时有积分因子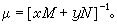
一阶隐方程 形如
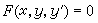(22)的方程称为一阶隐方程。当x、y的值固定时，一般由(22)可以解出不止一个的y′的值，这表示往往有多于一条的积分曲线经过(x，y)空间的一定点。特别，如果对于某一曲线Г上的每一点(x，y)，由(22)式解得的y′都有重根，并且Г本身也是(22)的积分曲线，则它往往就成为(22)的奇解。一般，Г也是(22)的积分曲线族的包络（有例外）。所以，求解隐方程(22)时经常在通解以外还可以得到奇解或包络。当求解由几何学所导出的隐方程时，目的往往是后者而非前者。若(22)可就y′解得若干个一阶显方程
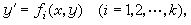(23)又能求得(23)中每一方程的通积分为Gi(x，y，C)=0，则(22)的通积分是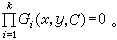
又若已知曲面F(x，y，z)=0有参数表示式:
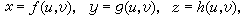则方程(22)等价于
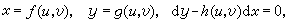由此可得u、v的一阶显方程
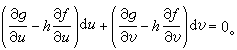(24)若ω（u，v，C）=0是(24)的通积分，则x=ƒ(u，v)，y＝g(u，v)，ω(u，v，C)=0是(22)的通积分。这种求解方法称为引入参数法。在求解(22)时，常记y′为p，且以p为参数来表达积分曲线族的方程。若由(22)可解得y=ƒ(x，p)或x=φ(y，p)，取x、p(或y、p)为参数即可把(22)化成(24)的形式。又若(22)取特殊形式
(25)则只要知道这种隐方程的参数表达式，由此导出的方程(24)必定是变量可分离的方程。如果存在常数k，使(22)中的函数F能满足
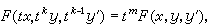则(22)称为广义齐次方程。这时可令x=et，y=zekt，而化(22)为
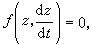即(25)的前一方程的形式。显然当k=1时(22)是比(4)更广的齐次一阶隐方程。一阶隐方程中，特别重要的是克莱罗方程
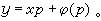(26)它的通解是y=Cx+φ(C)，表示一族直线；而奇解恰好是此直线族的包络。方程(26)之所以重要是因为几何学中要找一条曲线，使它的任一切线都具有某种与切点无关的性质，则所得的正是形如(26)的方程，其中x、y为实变量。有时对方程(22)可使用勒让德变换Χ=y′， Y=xy′-y将方程变形。此变换的逆变换也具有同样的形式:
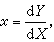
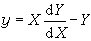；称为对称原理。当两方程F(x，y，p)=0与F(P，ΧP-Y，Χ)=0中的任一个可求积时，另一方程的通解便可借代数方法由前一方程的通解导出。这种变换在微分方程的理论研究中也很有用处。对于方程(22)，由F(x，y，p)=0及
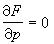消去p得到的关系式φ(x，y)=0，称为(22)的p-判别式。设(22)的通积分为φ(x，y，с)=0， 则由φ(x，y，с)＝0及
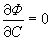消去C而得到的关系式ψ(x，y)=0称为(22)的C-判别式。如果(22)的奇解或积分曲线族的包络存在的话，其方程必同时含于p-判别式和C-判别式之中，但其逆不一定成立。一个典型的例子是
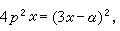(27)其通积分为
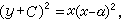C-判别式为x(x-α)＝0，p-判别式为
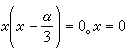是奇解，也是积分曲线族的包络。但x=α是结点轨迹，不是(27)的解；
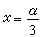是切点轨迹，也不是(27)的解。若α=0，则x=0成为积分曲线族
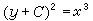的尖点轨迹，它也不是方程4p2=9x的解。高阶方程 一般形式为
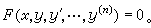(28)这类方程中比较典型的可求通积分或可降阶的有以下几种：①y
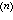=ƒ(x)，对 x积分n次即得通解。②y″=ƒ(y)，此方程有明显的物理学意义。以 2dy乘之，积分，得：
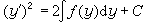它表示能量守恒律，再积分即得通解。③F(x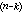，y
，…，y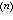
)＝0可借代换z=y
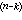降阶k次。④F(y，y′，…，y
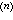)=0，可改取y为自变量，y′=p为未知函数而降阶一次。⑤ F(x，y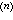)＝0，若能找到方程的参数表示式x＝φ(t)，y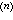=ψ(t)，便可将y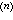逐次对x积分而得出通解的参数表示式。⑥若F 对 y，y′，…，y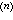为齐次函数，即F(x，ty，…，ty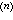)=tmF(x，y，…，y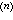)，则可借代换z=y′/y而把（28）降阶一次。⑦像一阶恰当方程一样，(28)有时也可表为
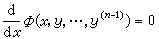的形式。积分一次，即可降阶为n-1阶方程，例如若 
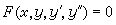(29)关于y″为线性，记 F(x，y，y′，y″)＝A(x，y，y′)y″+B(x，y，y′)，视x、y为常数，将A对y′积分，记其原函数为G(x，y，y′)，设
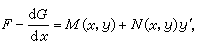且M、N满足条件(18)，则(29)即为恰当方程。特别，二阶线性方程 y″+p(x)y′+q(x)y+r(x)=0，当q(x)=p′(x)时为恰当方程。方程组的初等积分法 方程组
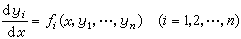(30)的初等积分法基本上依赖于前面讲过的两种方法的合并使用，即，①经过方程之间的组合以构成可积方程；②利用已经得到的积分（称为首次积分）来减少未知函数的个数。只要能得到n个独立的首次积分，它们合在一起就构成了(30)的通积分。为了实现①，往往把(30)改写成
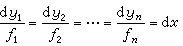的形式，然后利用比例的性质得到分子与分母的有用的组合。例如对
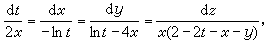(31)由第一等式和前两个等式不难得到两个独立首次积分:
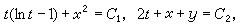再用后一等式代入(31)的最后一项，令与第一项相等，又可积得 
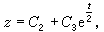它和前两个首次积分一起就构成(31)的通积分。有时用不同的方法可得不同的首次积分，但可证明(30)的独立的首次积分最多只有 n个。又若能用上述方法求得(30)的k个独立的首次积分，就可以利用它们来把(30)降为只 含n-k个未知函数的方程组。一般，由实际问题导出的方程组要想用初等积分来求得通解往往是办不到的。例如在天体力学中，由三体问题建立的一阶方程组含有18个方程，而人们只能找到它的10个独立的首次积分。即使对平面限制性圆形三体问题的最简单情况，通积分也还未求出来。