固体的能带(卷名:物理学)
energy bands of solids
现代物理学描绘固体中原子外层电子运动的一种图像。当原子互相靠近结成固体时,各个原子的内层电子仍然组成围绕各原子核的封闭壳层,和孤立原子一样;然而,外层价电子则参与原子间的相互作用,应该把它们看成是属于整个固体的一种新的运动状态。
能带的基本概念 1928年,F.布洛赫首先运用量子力学的原理来分析晶体中的外层电子的运动。他指出,由于晶体中原子作规则排列,电子是在一个周期势场中运动。单个电子的波函数嗞(k,R)应该满足薛定谔方程:
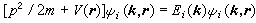 , (1)式中势能
, (1)式中势能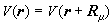 , (2)Rμ是晶体的任一点阵矢:
, (2)Rμ是晶体的任一点阵矢: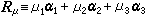 , (3)式中α1、α2、α3是点阵的基矢,μ1、μ2、μ3为整数。布洛赫证明,满足方程(1)的解具有一般形式
, (3)式中α1、α2、α3是点阵的基矢,μ1、μ2、μ3为整数。布洛赫证明,满足方程(1)的解具有一般形式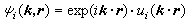 , (4)式中
, (4)式中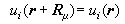 (5)是一个和V(r)同周期的函数。这个论断称为布洛赫定理,形式如式(4)的波函数称为布洛赫函数,它反映晶体中电子运动的基本性质。式(1)的本征值Ei(k)代表在周期性势场中单电子态的能量。其中k为波矢,它的变化范围限制在波矢空间的一个多面体之内,这多面体称为布里渊区,其形状和大小由晶体结构决定。下标i是本征能量的序号,第i个Ei(k)所确定的能量范围称为第i个能带。按照泡利不相容原理,每个能带可容纳晶体元胞数目二倍的电子。晶体电子按低能态到高能态的顺序填充能带。价电子所处的能带以及能量更高的空带同固体的许多物理和化学性质密切有关。
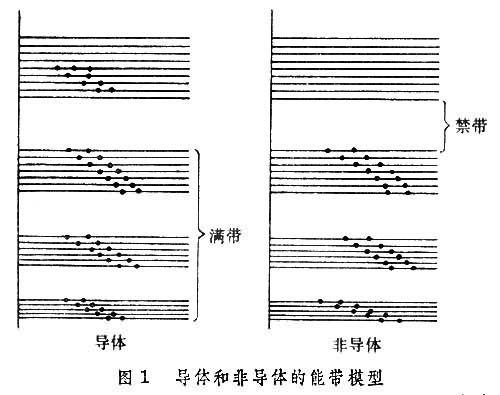
(5)是一个和V(r)同周期的函数。这个论断称为布洛赫定理,形式如式(4)的波函数称为布洛赫函数,它反映晶体中电子运动的基本性质。式(1)的本征值Ei(k)代表在周期性势场中单电子态的能量。其中k为波矢,它的变化范围限制在波矢空间的一个多面体之内,这多面体称为布里渊区,其形状和大小由晶体结构决定。下标i是本征能量的序号,第i个Ei(k)所确定的能量范围称为第i个能带。按照泡利不相容原理,每个能带可容纳晶体元胞数目二倍的电子。晶体电子按低能态到高能态的顺序填充能带。价电子所处的能带以及能量更高的空带同固体的许多物理和化学性质密切有关。能带的图像(图1)可以说明金属、半导体和绝缘体的区别。金属都有部分被电子占据的宽能带,称为导带,在这种能带中空着的电子态的能量与被占的态相连接,能带填充情况很容易被电场作用所改变,表现出良好的导电性。绝缘体则是另一种极端情况,电子恰好填满最低的一系列能带,其最高的满带有时称为价带,更高的各能带都空着。满带与空带之间隔着较宽的禁带,电场很难使能带的填充情况改变,因而不产生电流。半导体的能带填充情况很像绝缘体,但是空导带与价带之间的禁带比绝缘体窄得多,因此可以引入杂质或热激发,使空导带出现了少数电子,或价带中出现少数空穴,或兼有二者,从而有一定的导电性。
对于某一个能带(略去序号i),E(k)是波矢的偶函数,即E(k)=E(-k)。在状态E(k)中的电子,具有平均速度
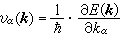 , (6)式中α为波矢空间的笛卡儿坐标符号。由此可知,一个能带中k和-k两个状态电子的能量相等,但平均速度数值相等而符号相反。
, (6)式中α为波矢空间的笛卡儿坐标符号。由此可知,一个能带中k和-k两个状态电子的能量相等,但平均速度数值相等而符号相反。在能带的极值点 (k=ko点)附近,价电子状态的能量可以写成
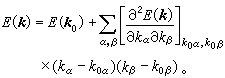 (7)由此可以规定电子的有效质量
(7)由此可以规定电子的有效质量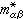
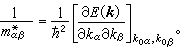 (8)一般说,晶体电子的有效质量
(8)一般说,晶体电子的有效质量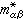 是一个二阶张量。在简单情况下,电子的有效质量m*为标量
是一个二阶张量。在简单情况下,电子的有效质量m*为标量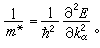 (9)有效质量反映了晶体周期性势场对电子的影响。晶体电子和自由电子的行为类似,两者的区别在于晶体电子用有效质量替代自由电子的惯性质量。
(9)有效质量反映了晶体周期性势场对电子的影响。晶体电子和自由电子的行为类似,两者的区别在于晶体电子用有效质量替代自由电子的惯性质量。固体的许多物理性质,例如电子的比热容、光吸收和光发射等都同态密度这个函数有密切的关系。态密度函数记作G(E),其定义是在能量E附近单位能量间隔内闪电子态的数目,即
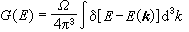 , (10)式中Ω为晶体元胞的体积,δ是狄喇克δ 函数,积分遍及整个布里渊区。
, (10)式中Ω为晶体元胞的体积,δ是狄喇克δ 函数,积分遍及整个布里渊区。在外加电场E和磁感应强度场B中,电子态以及电子的平均速度都要变化。在外加场较小的情况,电子的运动服从经典的规律:
 。 (11)所以在有效质量是二阶张量的情况,电子的加速度方向和外场力的方向不一致,只有在晶体电子有效质量m*为标量的简单情况,电子加速度和外场力的方向相一致。
。 (11)所以在有效质量是二阶张量的情况,电子的加速度方向和外场力的方向不一致,只有在晶体电子有效质量m*为标量的简单情况,电子加速度和外场力的方向相一致。波函数ψi也可以改写成另一种形式:
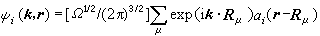 , (12)式中Ω是晶体元胞的体积,而
, (12)式中Ω是晶体元胞的体积,而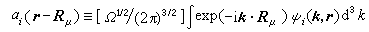 (13)是一个以阵点Rμ为中心的局域性函数,称为万尼尔函数。
(13)是一个以阵点Rμ为中心的局域性函数,称为万尼尔函数。计算方法 能带结构是决定固体各种特殊物理性质的重要因素,对具体材料的能带进行理论计算和实验研究一直是半个世纪来固体物理中的一个重要的基础性课题。到目前为止,人们已对各种简单金属、半导体及许多包含 d电子的过渡金属及其结构比较简单的化合物的能带结构作了较可靠的理论计算,与实验观测基本相符。近年来,对于f电子的稀土金属、锕系金属以及较复杂结构化合物的能带结构的研究也正在发展中。
严格计算三维晶体点阵中的单电子波函数嗞i(k,R)在数学上是极困难的。到目前为止,人们只能求得它的不同精确程度的近似解。下面简要介绍计算固体能带的一些理论方法。
紧束缚近似 布洛赫在1928年首先提出一个描写晶体单电子波函数的紧束缚近似。他考虑电子在阵点Rμ附近主要是受到Rμ原子场的作用。因此仍然可以用在Rμ处的孤立原子中的电子束缚态嗞i(R-Rμ)来近似地描述。然而,电子又可以在整个晶体中作共有化运动,所以对整个波函数 嗞i(k,R)可以取各个阵点原子的束缚态的线性组合来作近似描述,也就是设
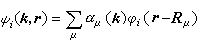 , (14)代入方程(1)得到
, (14)代入方程(1)得到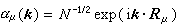 , (15)
, (15)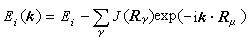 , (16)式中J(Rγ)称为重叠积分,它在这种近似描述中反映相距Rγ的两个原子对外层电子i的影响。
, (16)式中J(Rγ)称为重叠积分,它在这种近似描述中反映相距Rγ的两个原子对外层电子i的影响。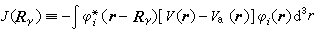 , (17)而Va(R)代表在孤立原子中电子i的势,Ei代表孤立原子中电子i的能级。
, (17)而Va(R)代表在孤立原子中电子i的势,Ei代表孤立原子中电子i的能级。由式 (16)可以看到电子i在晶体中作共有化运动时其能量与孤立原子中的能量Ei有所不同,它随着波矢k而变化。这样,对应于孤立原子中的一个量子态i,在固体中有由N个间隔很近的能级组成的“带”,称为“能带”,如图2所示。能带的宽度取决于重叠积分J(Rγ),如果各不同原子的波函数之间的重叠愈多,由式(17)可见重叠积分 J(Rγ)的值会愈大,能带也愈宽。原子内层的电子轨道很小,在不同原子之间很少重叠,因此能带很窄,而外层电子的轨道在不同原子间重叠很多,所对应的能带也较宽。在两个能带之间没有电子态的能量区间称为禁带。
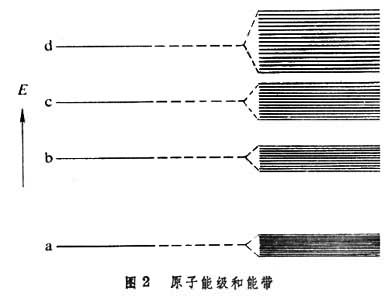
上面讲到的紧束缚近似又称为原子轨道线性组合法。它一般运用于不同原子之间轨道重叠较少的窄禁带固体。
近自由电子近似 也可从另一方向来近似描述固体中的电子运动,把式(1)中的周期势V(r)分成两部分:
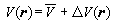 , (18)式中堸是一个常数, 是V(r)的平均值。把式(12)代入式(1)并且把ΔV(r)看成微扰势,采用平面波作嗞(k,R)的零级近似,用微扰论处理就得到电子能谱的各级近似:
, (18)式中堸是一个常数, 是V(r)的平均值。把式(12)代入式(1)并且把ΔV(r)看成微扰势,采用平面波作嗞(k,R)的零级近似,用微扰论处理就得到电子能谱的各级近似: , (19)式中
, (19)式中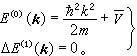 (20)如果对所有不为零的倒易点阵矢量Gt都有
(20)如果对所有不为零的倒易点阵矢量Gt都有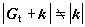 的关系,则
的关系,则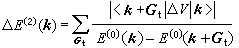 , (21)电子的能谱与自由电子十分近似。但是在布里渊区边界面上有
, (21)电子的能谱与自由电子十分近似。但是在布里渊区边界面上有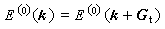 时,上述微扰方法不能使用,需用简并微扰论来求E(k)。可以证明,在这种波矢k的附近E(k)会出现一个“能隙”(图3),也就是禁带。以上这种处理方法称为近自由电子近似,它所给出的图像与对简单金属的实验观测基本相合。
时,上述微扰方法不能使用,需用简并微扰论来求E(k)。可以证明,在这种波矢k的附近E(k)会出现一个“能隙”(图3),也就是禁带。以上这种处理方法称为近自由电子近似,它所给出的图像与对简单金属的实验观测基本相合。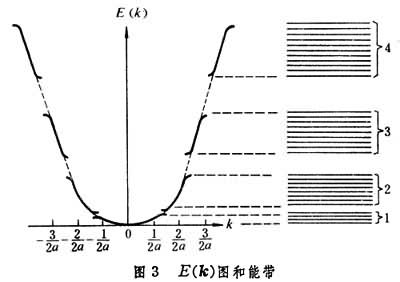
正交化平面波法 但是,如果考虑晶体势ΔV(r)大体相当于离子实对电子的库仑势,它在阵点附近的涨落是很大的,如果用平面波来展开布洛赫函数,就必须考虑许多包含各种Gt的项,在计算上是很困难的。
C.赫林在1940年建议用一套与各原子的内层电子轨道都互相正交的平面波ⅹ(k,r)来代替平面波作为描写电子波函数嗞(k,r)的基:
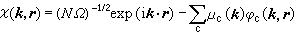 , (22)式中嗞c是原子内层(离子实)的电子波函数,μc(k)是系数,它由正交条件
, (22)式中嗞c是原子内层(离子实)的电子波函数,μc(k)是系数,它由正交条件 (23)决定。以函数ⅹ(k,r)为基的处理方法称为正交化平面波法。用这种方法对半导体和简单金属的能带进行计算时,收敛性比以前好得多,取得了很大的成功。这是因为正交化平面波比单纯的平面波更接近固体中共有化电子的实际运动。
(23)决定。以函数ⅹ(k,r)为基的处理方法称为正交化平面波法。用这种方法对半导体和简单金属的能带进行计算时,收敛性比以前好得多,取得了很大的成功。这是因为正交化平面波比单纯的平面波更接近固体中共有化电子的实际运动。赝势法 如果把正交化平面波的式(22)代入晶体的薛定谔方程(1),就可以得出如下的表达式:
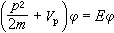 , (24)式中嗞代表式(22)等式右方第一项的平面波部分,因为它总是和正交化平面波ⅹ一一对应的,可以把它用作代表实际波函数的某种赝波函数。式中其余新符号的定义是:
, (24)式中嗞代表式(22)等式右方第一项的平面波部分,因为它总是和正交化平面波ⅹ一一对应的,可以把它用作代表实际波函数的某种赝波函数。式中其余新符号的定义是: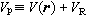 , (25)
, (25)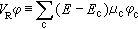 , (26)
, (26)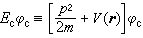 。 (27)
。 (27)这样,可以看到在这个晶体的薛定谔方程的新形式(24)中,起势能作用的是赝波函数中的Vp,通常把它称为赝势。它是由库化势V(r)与VR两部分组成。从(26)式可以定性地看出,由于传导电子的本征能量E比大体相当于离子实电子的能量的Ec大得多,VR的作用相当于一个强的排斥势。有时它可以在很大程度上抵消离子实区域的强吸引库仑势V(r)。于是作用于赝波函数中的赝势Vp远比作用在实际电子波函数的实际库仑势V(r)弱,因此方程(24)可以只用不太多的平面波的叠加来表达赝波函数中, 以及解出相应的晶体传导电子的能谱E(k)。当然,从理论上按式(26)严格计算赝势是繁难的。但是在实用中可以选用含有可调节的经验参量的各种简单的近似式来给出Vp。最后由比较计算结果与实测的晶体或原子数据来确定这些经验参量的具体数值。所以,根据方程(24)计算固体能带,实质上是一种半经验方法。它在近二十年来得到很广的应用。
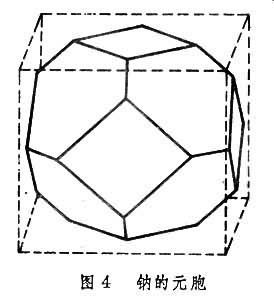
元胞法 E.P.维格纳和F.塞茨1933年提出一个计算固体能带的元胞法。他们把整个晶体划成分属于各个原子的许多“元胞”。每个元胞以阵点为中心由与近邻阵点连线的正交等分面围成,对体心立方的金属钠,元胞形状如图4。因为电子之间有很强的互斥作用,可以设想两个价电子同时处在一个钠原子元胞内的几率极小,所以可以近似地假定价电子所感受的势V(r)只是该元胞中心的离子实势。而别的元胞的离子实及其余价电子对它的作用势几乎互相抵消。这样,计算因体钠中电子波函数的薛定谔方程就和钠原子问题一样,所不同的是边界条件。在固体中必须保证波函数在元胞边界上平滑连续,并且遵守布洛赫定理。正是这种多边形边界条件很难作具体计算。他们对于比较简单的钠曾近似地把元胞当作球形来计算,但对比较复杂的金属就不能这样作了。
缀加平面波法 J.C.斯莱特1937年提出一个与元胞法类似的缀加平面波法。假设元胞中的势V(r)可以用一个在中心区的球对称原子势V(r)和在边角区的平势来近似描述。即在元胞里作一个半径ri的球,设
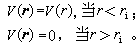 (28)这种形式的势称为丸盒势。因此波函数在球内应是各种角动量的原子波函数的线性组合,而在球外边角区斯莱特把波函数描述为平面波的组合,两者在各球面连续结合并满足布洛赫定理。后来J.科林加、W.科恩和N.罗斯托克提出把各元胞边角区的电子波函数用由各原子散射的球面波的组合来描述,通常简称KKR方法。这些方法都吸收了元胞法的优点,同时又利于处理边界条件。近年来在各种实际固体,特别是包含d电子的过渡金属及其化合物的能带计算中得到广泛的应用。
(28)这种形式的势称为丸盒势。因此波函数在球内应是各种角动量的原子波函数的线性组合,而在球外边角区斯莱特把波函数描述为平面波的组合,两者在各球面连续结合并满足布洛赫定理。后来J.科林加、W.科恩和N.罗斯托克提出把各元胞边角区的电子波函数用由各原子散射的球面波的组合来描述,通常简称KKR方法。这些方法都吸收了元胞法的优点,同时又利于处理边界条件。近年来在各种实际固体,特别是包含d电子的过渡金属及其化合物的能带计算中得到广泛的应用。