亦称“峰态系数”。设随机变量X的数学期望与方差分别为EX和var(X)≠0,则称
为X的峰度。它是反映X的密度函数曲线在众数附近的“峰”的尖峭程度的数字特征。正态分布的峰度为0,其他分布的峰度是以正态分布为标准描述该分布密度形状为陡峭或平坦的数字特征。

出处:管理学卷 • 统 计 学 • 概率论
| 词条 | 峰度 |
| 释义 | 峰度 峰度 亦称“峰态系数”。设随机变量X的数学期望与方差分别为EX和var(X)≠0,则称 为X的峰度。它是反映X的密度函数曲线在众数附近的“峰”的尖峭程度的数字特征。正态分布的峰度为0,其他分布的峰度是以正态分布为标准描述该分布密度形状为陡峭或平坦的数字特征。  出处:管理学卷 • 统 计 学 • 概率论 峰度 亦称“峰态系数”。数理统计中表示分配数列的峰度即其算术平均数邻近变量值分布的集中程度的数值。计算公式为: 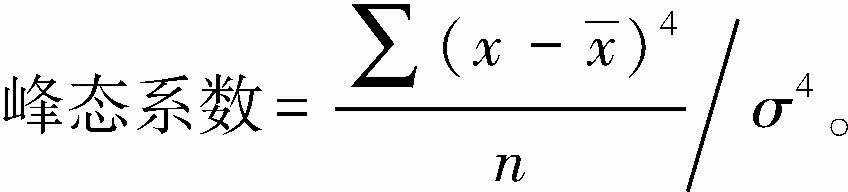 式中,∑为总计的符号,x为变量, 式中,∑为总计的符号,x为变量,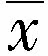 为算术平均数,n为变量值的个数,σ为均方差。正态分布的峰态系数为3,峰态系数大于3时,表示算术平均数邻近变量值分布比正态分布更集中;峰态系数小于3时,表示算术平均数邻近变量值分布比正态分布更分散。 为算术平均数,n为变量值的个数,σ为均方差。正态分布的峰态系数为3,峰态系数大于3时,表示算术平均数邻近变量值分布比正态分布更集中;峰态系数小于3时,表示算术平均数邻近变量值分布比正态分布更分散。出处:经济卷 • 统计学 • 统计学理论和方法 • 统计指标 |
| 随便看 |
百科全书收录258893条中英文百科知识,基本涵盖了大多数领域的百科知识,是一部内容开放、自由的电子版百科全书。