central limit theorem
mathematics
in probability theory, a theorem that establishes the normal distribution as the distribution to which the mean (average) of almost any set of independent and randomly generated variables rapidly converges. The central limit theorem explains why the normal distribution arises so commonly and why it is generally an excellent approximation for the mean of a collection of data (often with as few as 10 variables).
The standard version of the central limit theorem, first proved by the French mathematician Pierre-Simon Laplace (Laplace, Pierre-Simon, marquis de) in 1810, states that the sum or average of an infinite sequence of independent and identically distributed random variables, when suitably rescaled, tends to a normal distribution. Fourteen years later the French mathematician Siméon-Denis Poisson (Poisson, Siméon-Denis) began a continuing process of improvement and generalization. Laplace and his contemporaries were interested in the theorem primarily because of its importance in repeated measurements of the same quantity. If the individual measurements could be viewed as approximately independent and identically distributed, then their mean could be approximated by a normal distribution.
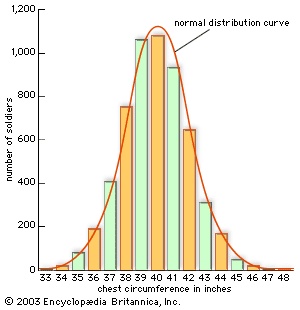 The Belgian mathematician Adolphe Quetelet (Quetelet, Adolphe) (1796–1874), famous today as the originator of the concept of the homme moyen (“average man”), was the first to use the normal distribution for something other than analyzing error. For example, he collected data on soldiers' chest girths (see figure-->
The Belgian mathematician Adolphe Quetelet (Quetelet, Adolphe) (1796–1874), famous today as the originator of the concept of the homme moyen (“average man”), was the first to use the normal distribution for something other than analyzing error. For example, he collected data on soldiers' chest girths (see figure--> ) and showed that the distribution of recorded values corresponded approximately to the normal distribution. Such examples are now viewed as consequences of the central limit theorem.
) and showed that the distribution of recorded values corresponded approximately to the normal distribution. Such examples are now viewed as consequences of the central limit theorem.The central limit theorem also plays an important role in modern industrial quality control. The first step in improving the quality of a product is often to identify the major factors that contribute to unwanted variations. Efforts are then made to control these factors. If these efforts succeed, then any residual variation will typically be caused by a large number of factors, acting roughly independently. In other words, the remaining small amounts of variation can be described by the central limit theorem, and the remaining variation will typically approximate a normal distribution. For this reason, the normal distribution is the basis for many key procedures in statistical quality control.
- Perrin, Ami
- Perrine, Charles Dillon
- Perrin, Jean
- Perron, Edgar du
- Perronet, Jean
- Perrot, Jules
- Perrot, Nicolas
- Perrot, Sir John
- Perry
- Perry, Antoinette
- Perry, Bliss
- Perry, Lee
- Perry, Lilla Cabot
- Perry, Matthew C
- Perry, Nora
- Perry, Oliver Hazard
- Perry, Ralph Barton
- Perryville, Battle of
- Perry, W.J.
- Perréal, Jean
- Persephone
- Persepolis
- Perseus
- Pershing, John J
- Persia