limit
mathematics
mathematical concept based on the idea of closeness, used primarily to assign values to certain functions (function) at points where no values are defined, in such a way as to be consistent with nearby values. For example, the function (x2− 1)/(x− 1) is not defined when x is 1, because division by zero is not a valid mathematical operation. For any other value of x, the numerator can be factored and divided by the (x− 1), giving x+1. Thus, this quotient is equal to 2 for all values of x except 1, which has no value. However, 2 can be assigned to the function (x2− 1)/(x− 1) not as its value when x equals 1 but as its limit when x approaches 1. See analysis: Continuity of functions (analysis).
One way of defining the limit of a function f(x) at a point x0, written as

is by the following: if there is a continuous (continuity) (unbroken) function g(x) such that g(x)=f(x) in some interval around x0, except possibly at x0 itself, then
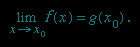
The following more-basic definition of limit, independent of the concept of continuity, can also be given:
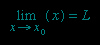
if, for any desired degree of closeness ε, one can find an interval around x0 so that all values of f(x) calculated here differ from L by an amount less than ε (i.e., if |x− x0|\\<δ, then |f (x)− L|\\<ε). This last definition can be used to determine whether or not a given number is in fact a limit. The calculation of limits, especially of quotients, usually involves manipulations of the function so that it can be written in a form in which the limit is more obvious, as in the above example of (x2− 1)/(x− 1).
Limits are the method by which the derivative, or rate of change, of a function is calculated, and they are used throughout analysis as a way of making approximations into exact quantities, as when the area inside a curved region is defined to be the limit of approximations by rectangles.
- flowering rush
- Flower, Lucy Louisa Coues
- flowerpecker
- Flower, Sir William Henry
- flowstone
- Floyd Bennett
- Floyd Dell
- Floyd Dixon
- Floyd, John Buchanan
- Floyd Patterson
- Floyd, Pretty Boy
- Fludd, Robert
- fluid
- fluidics
- fluid mechanics
- fluke
- Flumendosa River
- fluorapatite
- fluorescein
- fluorescence in situ hybridization
- fluorescence photography
- fluorescent lamp
- fluoride deficiency
- fluorine
- fluorite