*康托尔在1878年提出的关于连续统基数的一个假设。通常称实数集 0
0 为希伯来字母,读作“阿列夫”
为希伯来字母,读作“阿列夫” 0之间有关系式C=2
0之间有关系式C=2 0;并把无穷基数按照从小到大的次序排列为:(+)
0;并把无穷基数按照从小到大的次序排列为:(+) 0,
0, 1,…,
1,…, α,…其中α为任意序数。康托尔猜想,2
α,…其中α为任意序数。康托尔猜想,2 0=
0= 1,即实数集的基数是自然数集基数
1,即实数集的基数是自然数集基数 0之后最小的无穷基数,这就是著名的连续统假设
0之后最小的无穷基数,这就是著名的连续统假设 α=
α= α+1成立,就称为广义连续统假设
α+1成立,就称为广义连续统假设
| 词条 | 连续统假设 |
| 释义 | 连续统假设 *康托尔在1878年提出的关于连续统基数的一个假设。通常称实数集 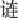 |
| 随便看 |
百科全书收录125729 条中英文百科知识,基本涵盖了大多数领域的百科知识,是一部内容开放、自由的电子版百科全书。