指数列1， 1， 2， 3， 5， 8， 13， 21，……。它的第1、第2项为1，从第3项起每一项等于它的前两项之和。通项公式是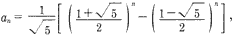前n项的和S_n=a_n+2－1，并且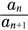是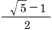的最佳渐近分数，因此在^*优选法中得到应用。这一数列是意大利学者斐波纳奇(Leonardo Fibonacci, 约1170—1240)因探讨下列问题而引进的：如果每一对大兔子每月生出一对小兔，而每一对新生的兔子第二个月也会生出一对，而且不发生死亡，那么由一对大兔子开始，一年后能有多少对?其答案正是斐波纳奇数列的第13项，且数列的各项依次给出了各个月大兔子的对数。