区间分析(卷名：数学)
interval analysis
又称区间数学，是一门用区间变量代替点变量进行运算的数学分支。它最初是从计算数学的误差理论研究发展起来的。1966年R.E.穆尔在《区间分析》一书中第一次系统提出区间运算理论。记I(R)为所有有限长区间总集合，即I(R)=｛[α，b)]│α≤b)，α，b)∈R｝，如果α=b)就是一个实数α=〔α，α〕称为点区间，设I，J∈I(R)为两区间，I=[α，b)]，J=[с，d]，可定义区间四则运算为
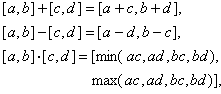
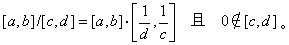
区间四则运算符合加法与乘法的交换律与结合律，但不符合乘法对加法分配律，而满足次分配律，即对I，J，K∈I(R)有
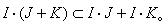符号I嶅J表示J包含I，I∩J表示区间之交，I∪J表示区间之并，它与集合运算规律相同。若I，J，K，L嶅I(R)且I嶅K，J嶅L则有
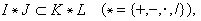称为区间运算的包含单调性。利用这一性质对任一有理函数ƒ(x)，可把点变量x换成区间变量x进行运算，这样得到的区间值函数F称为ƒ的区间扩展函数。在n维空间中，若向量x＝(x1，x2，…，xn)的分量xj(i=1，2，…，n)都是区间，则x称为n维区间向量，几何上表示n维长方体。若n×m阶矩阵A的元素Aij都是区间，则A＝
称为区间矩阵。对区间向量和矩阵也可定义它们的运算及范数。此外还可定义区间映射、区间导数、区间积分等等，它们构成区间分析的基本内容。将区间运算与其他数学领域相结合就形成了区间代数、区间几何等等。20世纪70年代以来区间数学有很大发展，在计算数学方面有很多应用，如利用区间迭代法可判断对非线性方程组及算子方程解的存在惟一性及区间迭代序列收敛性，这是点迭代法得不到的结果。此外，它在区间插值与逼近、线性方程、非线性规划、微分方程等方面也有应用。直接用区间量计算的计算机语言──区间语言也已出现。
参考书目
R. E. Moore，Interval Analysis，Prentice-Hall， Englewood Cliffs， New Jersey， 1966.