场论(卷名：数学)
theory of fields
向量分析在数学、物理各分支中的一种非常有用的理论。
数量场与向量场 定义在空间某确定范围内每一点处的某种物理量称为一个场。用数学术语讲，就是在该范围内定义了一个点函数。不过这种量（函数值）可以是数量（如温度、电位等），也可以是向量（如速度、引力等）。前者称为数量场，后者称为向量场，分别记为u(P)与a(P)，这里P是定义范围内的动点。
在空间引进一直角坐标系Oxyz，P点就有坐标(x，y，z)，于是数量场u=u(P)就可写成
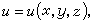(1)向量场A=A(P)就可写成A=A(x，y，z)
={Ax(x，y，z)，Ay(x，y，z)，Az(x，y，z)}。 (2)它们分别就成为三个变量的数量函数与向量函数。引进坐标系，是为了便于对它们进行运算和数学处理，而场本身的性质是与坐标系的选取无关的。
下面恒假定以上所遇到的函数在场内都有连续偏导数，这种场也称为光滑场。
梯度 已给一数量场(1)，定义一个向量函数
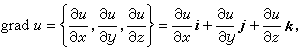(3)称为u的梯度，式中i、j、k分别为沿x轴、y轴、z轴正向的单位向量。这向量的方向指向u(P)增长最快的方向，其模(大小)就是这一最大增长率。所以向量函数(3)虽以坐标形式给出，但它本身却与坐标系的选择无关。以向量函数(3)构成的向量场，称为梯度场(grad是gradient的缩写，是“倾斜”的意思)。引进一个形式向量的记号
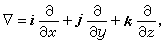则(3)就可简写成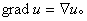
一个向量场A， 如果它是某数量场 u的梯度场 A＝grad u，则称a是一位势场，而u称为其位势。
散量 已给一向量场(2)，引进一数量函数
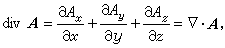(4)称为A的散量（或散度）。在场内任取一立体区域V，其边界为一光滑曲面S，S上任意点的外法线单位向量记为n，则多元微积分中的奥斯特罗格拉茨基公式可以写成向量形式
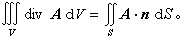如果把A 看成是场中流体稳定流动的速度，则此式右边表示流体通过曲面S流出去的流量，因此divA表示流体在场中各点发散的密度。前者是与坐标选择无关的，所以后者也是如此。因此，divA构成一个数量场，称为a的散量场（div是divergence的缩写，是“发散”的意思）。在某点P 处divA>0，表明流体在该处有一源（有流体喷射到场内）；divA<0，则表明流体在该处有一汇（有流体渗漏出场外）。如果diva呏0，则称A为一管量场。
旋度 已知一向量场(2)，定义一向量函数
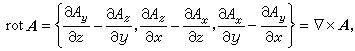(5)称为A的旋度。在场中取一光滑曲面片S，其边界为一光滑封闭曲线L 。取定S的一侧作为正侧，正侧法线的单位向量记为n；由此诱导L的一正向，正向切线的单位向量记为t，则斯托克斯公式可改写为
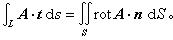如前把A理解为流体速度，则此式左边刻画着流体沿L转动的程度，是与坐标无关的。由此也可证明rotA也与坐标选择无关：其方向表明流体在一点附近绕怎样的轴旋转，其模则刻画着旋转的(角)速率之半。这就是说 rotA也是一个向量场，称作A的旋度场(rot是rotor的缩写，是“转动”的意思），也可记作curlA（curl是“鬈曲”的意思）。如果rota呏0，则称a为一无旋场。
可以证明，无旋场与位势场这两概念是等价的。
如果不用直角坐标系，而改用别的正交坐标系，则梯度、散量、旋度也有相应的表达公式，不过一般比较复杂。