方差分析(卷名：数学)
analysis of variance
分析实验数据的一种重要的数理统计学方法。其要旨是对样本观测值的总变差平方和进行适当的分解，以判明实验中各因素影响的有无及其大小。这是由R.A.费希尔1923年首创的。设Y1，Y2，…，Yn为n个观测值，
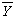为平均值，称
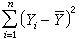为Y1，Y2，…，Yn的变差平方和，简称总平方和，它反映观测值在平均值上下波动的大小。当观测值受到多种因素的影响时，每一因素都对平方和的值有影响，若能从平方和中分解出反映某一因素影响的那一部分(也用平方和的形式表示)，则由这部分的大小就可以推断该因素的影响是否显著。但是，若试验未经适当的设计，则所产生的数据难以进行平方和分解与相应的统计推断。因此方差分析和实验设计法是密切相关的，不同的实验设计相应于不同的方差分析形式，而方差分析理论对实验设计的选择又有指导作用。例如，进行一项作物品种与肥料的农业试验，品种和肥料就是所考虑的两个不同的因素，而各因素的不同取“值”，称为该因素的水平。假定有α个品种A1、…、Aα与b种肥料B1、…、Bb供选取，在水平Ai和Bj的组合条件下的试验称为一个处理。在这试验中，全部可能的处理数目共有αb个，即为因素A（品种）与因素B（肥料）的各自水平数的乘积。设每个处理种r块试验田，以Yijk)记用第i个品种、第j种肥料在第k个重复试验的地块上所得试验的亩产量，对不同的(i，j，k)，Yijk)之值各不相同，它的总变差平方和为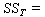
(
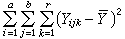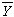是全部Yijk)的平均值)，它反映了品种、肥料以及随机误差(它包含土壤的不均匀性等大量的不可控因素)的影响，通常又称总平方和。在这种两因素试验情况下总平方和可以分解为四部分
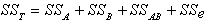， (1)式中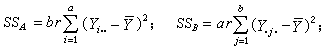
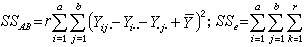(Yijk)-Yij.)2，而Y
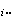为固定i对一切j、k求Yijk)的平均值，Y.j.与Yij.有类似的含义。SSA和 SSB分别反映因素A和B各自对SST的贡献，分别称为因素A和B的主效应平方和。SSAB反映由因素A、B的相互影响而对SST的贡献，称为A、B的交互效应平方和。SSe反映随机误差的影响，通常称误差平方和。每项平方和都对应着一个“自由度”，就上例而言，SSA、SSB、SSAB、SSe的自由度分别为α-1、b-1、(α-1)(b-1)和αb(r-1)。 分别记之为ƒA、ƒA、ƒe和ƒe。总平方和SST的自由度 ƒT定义为总的观测次数减去1，即αbr-1，它恰好是ƒA、ƒA、ƒe和ƒe之和，即有类似于(1)的分解式
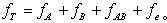(2)平方和除以各自的自由度称为均方，记为M S，例如
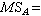SSA/(α-1)，等等。诸因素效应的大小，用它的均方与误差均方的比值(记为F)的大小来衡量，例如，FA=M SA/M Se，反映因素 A的主效应对亩产的影响；FB＝M SB/M Se反映因素B 的主效应对亩产的影响；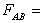
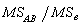则反映 A与B交互效应对亩产的影响。综上结果，可以列成一个方差分析表（表
）。前述例子的模型可写为
Yijk)=μ＋αi＋βj＋γij＋εijk)， (3)式中i=1，…，α；j=1，…，b；k=1，…，r；μ称总平均；αi、βj分别称品种(A)与肥料(B)的主效应，γij称A、B的交互效应，并且满足约束条件：
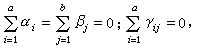
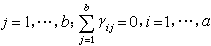。εijk)是随机误差。这是一个以μ、αi、βj及γij(i=1，…，α；j=1，…，b)为参数的线性模型(见线性统计模型)。“品种无主效应”这个假设，可表为 HA:αi=0，i=1，…，α，这是一个线性假设。在随机误差εijk)独立、等方差及正态假定下，可用似然比（见假设检验）方法检验这个假设，所得检验统计量正是上表中的FA=M SA/M Se，它是自由度为ƒA与ƒe的F 统计量。类似地可检验 
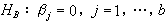和
在检验假设被拒绝后，就有估计效应及对之排序等问题，解决这种问题的工具是线性模型的估计理论以及多重比较的方法。
上例是一个典型的两种方式分组的方差分析问题，所谓“两种方式”即指按品种和肥料两个因素将试验数据分成αb组。一般地有多种方式分组问题。上例中涉及的品种等都是特定的，因此模型(3)中的效应看作固定参数，故称固定效应模型。如果讨论“品种对产量的影响”这种抽象形式的问题，这时设想有一个无限品种的集合，试验中所涉及的α个品种，只是作为全体品种的代表从品种集合中随机抽出的，这时模型(3)中效应不能看成一个参数而应看作随机变量。若所有效应均为随机变量，则称随机效应模型。若模型中兼有固定和随机两种效应，则称混合效应模型。一般，随机效应模型的方差分析在形式上与固定效应大体一致，但在作F检验(见假设检验)时有一些差别。
方差分析的思想也用于回归分析的假设检验。若在方差分析模型中有未加控制的系统性因素出现，则得到协方差分析模型。如上例，根据在生长期间各试验地块虫害的轻重程度，施用不同量的农药，记X为农药用量，它可能是影响产量的系统因素，如模型中不加考虑，必将降低分析精度。考虑的方法是在模型 (3)中加进一项反映该因素影响的量δXijk)，即
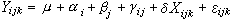，式中Xijk)为第i个品种、第j种肥料、第k个重复地块上的使用农药量。δ 为待估的回归系数。上述模型仍是一个线性模型，只不过模型中有连续取值的回归变量X和离散取值的方差变量A和B。因此，协方差分析可看成回归分析与方差分析的结合。参考书目
H.cheffe，The Analysis of variance，John Wiley & Sons，New York， 1959.