拉普拉斯无旋运动(卷名：力学)
Laplaceˊs irrotational motion
流场中各点墷×v=
的不可压缩流体运动，其中v为速度矢量。除极个别的特例外，粘性流体一般都作有旋运动。无粘性流体运动可以是有旋，也可以是无旋的。当流体是无粘性的、正压的（见正压流体）且外力有势时，均匀来流绕物体的流动和从静止起动的流体流动必定是无旋的（见开尔文定理）。这两类流动在工程中具有重大实际意义。对于不可压缩流体的无旋运动，流体力学基本方程组可以大为简化。考虑无粘性不可压缩流体的无旋运动。首先因墷×v＝
，所以存在速度势ф，使得v=墷ф，代入连续性方程得墷·(墷ф)＝
ф＝0，即速度势满足经典的拉普拉斯方程。其次，拉格朗日积分（见伯努利定理）成立：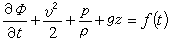
，式中v为速度；p为压力；ρ为流体密度;z为垂直高度;g为重力加速度；f(t)为待定的任意函数。于是问题化为：先解拉普拉斯方程，求出ф，然后按v=墷ф求出速度v，代入拉格朗日积分即可求出压力p。 处理无粘性不可压缩流体的无旋运动，数学上的简化主要体现在以下几点：①有旋运动时的非线性运动方程现在可以积分出来变成非线性的有限关系式──拉格朗日积分，而确定速度矢量v的连续性方程在加上无旋条件后变成了确定调和函数ф的线性拉普拉斯方程，对于拉普拉斯方程的性质和解已经研究得很清楚了；②有旋运动中v和p相互影响，必须一起解出， 现在运动学函数ф（也即v）和动力学函数p已可分开求解；③方程和未知函数的个数由四个降至两个。无粘性不可压缩流体的无旋运动具有下列性质：①速度的大小不能在流体内部达到极大值；②压力不能在流体内部达到极小值；③在边界上，若无旋运动和有旋运动具有相同的法向速度分量，则单联通区域内无旋运动的动能小于有旋运动的动能(见开尔文最小能量定理)。
对于不可压缩流体的平面运动还存在着流函数Ψ，它也满足拉普拉斯方程。势函数ф和流函数Ψ之间由柯西-黎曼条件联系起来，因而以ф为实部，Ψ为虚部组成的复变函数ω(z)是解析函数，称为复位势。于是，平面无旋运动的数学提法可叙述为：求流动区域内的解析函数ω(z)，它在区域内及边界上连续且满足物面及无穷远处的边界条件。
对于不可压缩流体的无旋运动，求解速度势ф或复位势ω(z)有以下几种方法：
①奇点分布法 根据速度势或复位势的叠加原理将均匀流、源流、点涡及偶极子流等基本流子按一定原则叠加起来，以解决各种绕流问题。这种方法物理概念清晰，比较直观，能够有效地解决不少问题。
②镜象法 此法适用于边界为无界平面、圆柱面或球面的情况。若已知平面、圆柱面或球面等边界不存在时流动问题的解，则利用映射定理、圆周定理和球定理可以容易地写出上述这些边界放入流动流体后新问题的速度势或复位势。
③保角映射法 复变解析函数理论为解决平面无旋流动问题提供了一个强有力的工具。黎曼定理指出在一定条件下将区域边界映射到圆上去的单值解析函数是存在且唯一的。如果具体地找到了这样的函数，则根据已知的圆柱绕流问题的解可以写出绕各种相应复杂边界流动问题的解。于是，问题便归结为如何具体地找出适当的映射函数。对于边界比较简单的流动可以容易地找出映射函数，对于复杂的边界，已经提出几种数值求解方法。
④数值计算方法 包括有限差分方法和有限元法等。它们的优点在于适应面广，可以解决包括复杂边界问题在内的各种绕流问题。