微分方程(卷名：数学)
differential equation
常微分方程与偏微分方程的总称。含自变量、未知函数和它的微商（或偏微商）的方程称为常（或偏）微分方程。微分方程论是数学的重要分支之一。它几乎和微积分同时产生，并随实际需要而发展。
微分方程研究的来源 它的研究来源极广，历史久远。I.牛顿和G.W.莱布尼茨创造微分和积分运算时，指出了它们的互逆性，事实上这是解决了最简单的微分方程 y′=ƒ(x)的求解问题。当人们用微积分学去研究几何学、力学、物理学所提出的问题时，微分方程就大量地涌现出来。例如，平面二次曲线方程含有五个参数，两端对x求五次微商，连同原方程共得六个方程，消去参数就得到微分方程
。 (1)又如曲面变形论提出了微分方程组
(2)几何学提出的微分方程很多。（J.-）G.达布的《曲面一般理论教程》一直是这方面值得参考的书。变分学中令积分取极值的必要条件欧拉方程一般是非线性微分方程（或组）。
刚体力学的基本方程就是一个微分方程组。流体力学的基本方程就是所谓纳维-斯托克斯方程，弹性力学的方程一般是高阶方程。电磁学提出了著名的拉普拉斯方程
，光学和声学提出了波动方程
，热学提出了热传导方程
，量子力学中提出了薛定谔方程
。20世纪以来，随着大量的边缘科学诸如电磁流体力学、化学流体力学、动力气象学、海洋动力学、地下水动力学等等的产生和发展，也出现不少新型的微分方程（特别是方程组）。70年代随着数学向化学和生物学的渗透，出现了大量的反应扩散方程。
从“求通解”到“求解定解问题” 数学家们首先发现微分方程有无穷个解。常微分方程的解会含有一个或多个任意常数，其个数就是方程的阶数。偏微分方程的解会含有一个或多个任意函数，其个数随方程的阶数而定。命方程的解含有的任意元素（即任意常数或任意函数）作尽可能的变化，人们就可能得到方程所有的解，于是数学家就把这种含有任意元素的解称为“通解”。在很长一段时间里，人们致力于“求通解”。但是以下三种原因使得这种“求通解”的努力，逐渐被放弃。
第一，能求得通解的方程显然是很少的。在常微分方程方面，一阶方程中可求得通解的，除了线性方程、可分离变量方程和用特殊方法变成这两种方程的方程之外，为数是很小的。高阶方程中，线性方程仍可以用叠加原理求解，即n阶齐次方程的通解是它的n个独立特解的线性组合，其系数是任意常数。非齐次方程的通解等于相应齐次方程的通解加上非齐次方程的特解，这个特解并且可以用常数变易法通过求积分求得。求齐次方程的特解，当系数是常数时可归结为求一代数方程的根，这个代数方程的次数则是原方程的阶数;当系数是变数时，则只有二种极特殊的情况（欧拉方程、拉普拉斯方程）可以求得。至于非线性高阶方程则除了少数几种可降阶情形(如方程(1)就是这几种情形都有的一个方程)之外，可以求得通解的为数就更小了。n阶方程也可以化为一阶方程组（未知函数的个数和方程的个数都等于 n）早已为人们所知，并且在此后起着一定作用，但对通解的寻求仍无济于事。
在偏微分方程方面，一阶方程可以归结为一阶常微分方程组，但是如上所述，一阶常微分方程组可以求得通解的还是很少的。高阶方程中几乎只有少数二阶方程（如
，以及
，当用瀑布法时在一系列不变量中有一个开始为零的情形，和少数极个别的非线性方程如rt-s2=0等等）可以求得通解。在线性情形，推广常数变易法则是杜阿美原理。任意高阶方程都可以归结为一阶方程组，但此时方程的个数（仍等于未知函数的个数）都远远大于原方程的阶数；任意高阶组当然也可以归结为一阶组（此时方程个数仍等于未知函数个数）却更加远远地大于原方程的阶数。但反之，一个一阶组并不一定可能归结为一个高阶方程(一个未知函数)，而常是归结为几个高阶方程。总之，如果把求通解看作求微商及消去法的某一类逆运算，那么，也和熟知的逆运算一样，它是带试探性而没有一定的规则的，甚至有时是不可能的（J.刘维尔首先证明黎卡提方程不可能求出通解），何况这种通解也是随着其自由度的增多而增加其求解的难度的。
第二，当人们要明确通解的意义的时候（在19世纪初叶分析奠基时期显然会考虑到此问题）就会碰到严重的含糊不清之处，达布在他的教学中经常提醒大家注意这些困难。这主要发生在偏微分方程的研究中。
第三，微分方程在物理学、力学中的重要应用，不在于求方程的任一解，而是求得满足某些补充条件的解。A.-L.柯西认为这是放弃“求通解”的最重要的和决定性的原因。这些补充条件即定解条件。求方程满足定解条件的解，称之为求解定解问题。
从理论上讲，若已知方程的通解，则只需选择其中的任意元素使之满足定解条件即可得出定解问题的解。而实际上这种选择往往是非常难的，更不用说求得通解的困难了。相反地，如果把出现在定解条件中的数据或多或少地变动一下都能求得方程的一个解，那么把这些数据作尽可能地变动时就可能求得方程所有的解即通解。就是采取了这种观点，柯西和K.（T.W.）外尔斯特拉斯几乎同时证明了常微分方程通解的存在性，而偏微分方程也从此得到了迅速的发展。
定解问题的定义和要求 方程（或称泛定方程）
是加在含m个自变量x1，x2，…，xm的未知函数u及其各阶偏微商上的一个关系，即若把u和由它而得的它的各阶偏微商（至少是方程中出现的）都代入F中，则所得结果对于Rm中的某区域Ωm的所有内点x1，x2，…，xm来说，都要求恒等于零；但对于Ωm的边界点来说，并不作这样的要求。至于定解条件当xm=0时
则是在Rm中(m-1)维流形xm=0上被满足的。这时，xm=0就称为支柱。xm=0有时是Ωm中的一个(m-1)维流形，有时就是Ωm的边界дΩm或дΩm的一部分。所谓当xm=0时有
，就是在Ωm 内当xm＝0附近任一点沿任一曲线趋近于xm＝0上任一点(x嬼，x嬽，…，x圛)时，u趋近于u0(x嬼，x嬽，…，x圛)。在这种理解下，P.班勒卫指出了这时u0(x1，x2，…，xm-1)应是连续的。定解条件当xm=0时，
，当然也应是在Rm中一(m－1)维流形xm=0上被满足的。这时，xm=0仍被称为支柱，但对微商取值的理解有两种：一是把它看作当xm趋近于0时
的极限。二是把它看作
当 xm趋近于0时的极限。显然，若第二种理解成立则第一种理解必然成立。反之则不尽然。应该指出，也可以用
或 
，
或更一般地用 Rm中任何一个(m-1)维流形来代替xm=0，它们这时也都被称为支柱。对函数取值和微商取值若要作上述理解，还需对支柱作必要的正规要求，例如支柱至少是一个若尔当流形等等。上述泛定方程和定解条件的理解，都可以推广到方程组。但是应该注意，一般只讨论方程个数和未知函数个数相等的情况，即定组的情况。凡方程个数大于未知函数个数的组称为超定组。凡方程个数小于未知函数个数的组称为欠定组。
一个方程或方程组的定解问题一旦提出，就产生下列三个问题。①存在性问题，即这个定解问题是否有解。②惟一性问题，即其解是否惟一。③连续依赖性问题，即解是否连续依赖于数据，亦即是否是数据的某阶连续泛函。
若定解问题的解是存在的、惟一的、连续依赖于数据的，则这个定解问题称为适定的。对它就可以进行计算。一般而言，只有适定问题计算才有意义。这样，微分方程的研究成果才能为实际所应用。
如果对上述三个问题的回答有一个是否定的，这个定解问题就称为不适定的。一般，不适定问题是原来用来刻画实际规律的数学模型不恰当，必须另建合适的数学模型。不适定问题也是需要研究的，这种研究有时会导致理论上的新发展。
定解问题研究的发展 对常微分方程最早提出的定解问题是柯西问题(C)：
柯西问题(C)是适定的，其根据是柯西定理：若ƒ(x，y)在｜x-x0｜≤α，｜y-y0｜≤b上连续，并满足李普希茨条件
，则柯西问题(C)在满足条件
下，存在惟一的连续依赖于y0的连续解。由于泛定方程的任一解当x=x0时总要取一个值y0，因此就可以提出柯西问题(C)。由于惟一性，这个柯西问题的解一定就是所考虑的解，所以柯西问题(C)的解就是泛定方程的“通解”。柯西利用L.欧拉早就提出的近似解法（所谓欧拉折线法）证明了当折线边数无限增加、边长无限缩小时，这些折线有一极限即(C)的惟一连续依赖于y0的解。这个方法称为柯西-李普希茨方法。若取消李普希茨条件，则用阿尔泽拉定理仍能证明解的存在性，但不能证明惟一性和连续依赖性。可见李普希茨条件的作用只在于保证解的惟一性。逐次逼近法导源于代数方程近似解法，刘维尔首先把它用于解沃尔泰拉积分方程，(C.-)É.皮卡才把它广泛应用于解常微分方程柯西问题(C)上，首先把柯西问题变为非线性沃尔泰拉积分方程，然后用逐次逼近法求解，结果完全和欧拉折线法的一样。
柯西定理在复数域仍成立:若ƒ(x，y)在｜x-x0｜<α，｜y-y0｜<b上为解析，则当
时，(C)是适定的。柯西利用长函数法证明了这个命题。这些都很容易推广到最一般常微分方程组（只需方程个数和未知函数个数相等）。无论是欧拉折线法，还是逐次逼近法（和它的变形压缩映像、不动点定理）都要求ƒ满足对y的李普希茨条件，其实这是把方程线性化并且对其系数进行估计。若所有ƒ对所有y都是线性的，则可以得到更精确而重要的结果，即线性常微分方程解的奇点只能来自系数的奇点。最简单的非线性一阶方程黎卡提方程的通解的形式是
（ƒ，g，d，e是确定函数，с是任意常数），就没有这个结果。由于一阶常微分方程的一般形式是F(x，y，y′)=0，要应用柯西定理，就必需应用隐函数理论解出y′。在不满足隐函数定理的条件的情况，常常就是产生奇解的情况。克莱罗方程就是一个最简单的例子。定解问题研究的开展，大大帮助了对奇解的了解。
柯西提出定解问题的时代也是复变函数论开始蓬勃发展的时代，“两个实域真理间的最短途径时常是通过一个复真理的”影响，这是当时特别流行的说法，复域里常微分方程理论（即复解析理论）得到了发展。从推广柯西定理的布里奥-布凯定理，从（J.-）H.庞加莱的工作到班勒卫、J.马尔姆奎斯特等人的工作，最引人注目的是在线性方程方面，从I.L.富克斯的结果开始一直到庞加莱的自守函数理论已很完整。但是在非线性方面显然没有取得如此令人满意的成果，其原因可能是多复变函数的奇点理论和解析开拓尚有待发展。
二阶常微分方程的柯西问题
不是泛定方程（E2）惟一可以提出的定解问题。人们还可以提出如下的边值问题（相当于二阶偏微分方程的狄利克雷问题）：(D1)：
这两个问题均可归结为线性积分方程。前者可归结为第二种沃尔泰拉积分方程，后者则是第二种弗雷德霍姆积分方程。沃尔泰拉方程可以看作弗雷德霍姆方程的特例，但不同的是后者有本征值、本征函数问题，而前者没有。边值问题和由它而引起的本征值、本征函数问题，不仅有理论上的价值，为人们提供很多特殊函数，而且有实用价值（特征值问题在大型建筑中必需考虑到）。在椭圆型偏微分方程的边值问题中同样也引起本征值和本征函数问题。
天体力学中提出的太阳系稳定性理论课题，促进了常微分方程大范围研究，但是柯西所得结果都是局部的、小范围的。如何把柯西所得结果推广到全局呢？在常微分方程解析理论中，人们曾利用解析开拓法把某些线性方程在全平面的解全部求出。由J.（-S.）阿达马在美国耶鲁大学的报告“庞加莱的科学研究工作”可知，庞加莱受E.伽罗瓦创立群的观点来处理代数方程的方法的影响，不是从一条积分曲线出发而是考虑所有积分曲线和它们间的相互关系。当然，庞加莱首先从考虑最简单的一阶方程
(3)出发，这里x，Y都是x，y的多项式（阿达马认为，x，Y是否是多项式不是重要的，重要的是它们为x，y的单值函数）。为了便于讨论在无穷远处的奇点，庞加莱作一球在上侧切xy平面于原点，然后以球心为投影中心把xy平面任何一点投影到球面上得轴对称的两点。在所有讨论中，t总假定是增加的，这样就保证了在平面上的正规点处只有一条积分曲线经过，并且只给出t增加的一个切线方向。在作了这些基本假定下，庞加莱提出了两个原则来实现他从伽罗瓦处吸取的思想。第一个原则，在上述球上任一正则点（使x=0，Y=0的实点是方程的奇点，其余都是方程的正则点）都只通过方程的一条积分曲线。这个原则是从柯西定理来的，并且阐明了所有解间的关系。第二个原则，在非解线L上任一点，人们可以说清楚方程(3)的任一解曲线将在哪一个方向截L，L就是无接触弧。这个原则也阐明了所有解间的关系。就是这两个原则，允许人们得到了一系列难以想象的大范围的结果，即所谓常微分方程定性理论。它推动了组合拓扑学基本理论的建立。高维的定性理论还有待发展。
在柯西的倡导下，人们从“求通解”的时代进入了“求解定解问题”的时代，随着庞加莱的定性理论，常微分方程又从“求解定解问题”的时代进入“求所有解”的时代。
稍后，D.伯克霍夫在动力系统方面开辟了一个新领域。近年来，由于拓扑方法的渗入，更加得到发展。苏联Α.М.李亚普诺夫在运动稳定性方面的工作，对天文学、物理学以及工程技术有广泛应用，极受重视。
此外，在考虑时滞问题时，人们还创立了差分微分方程。近年来，泛函微分方程有很大发展。泛函微分方程是差分微分方程的推广。
柯西曾把他有关常微分方程方面的结果推广到一阶偏微分方程组的柯西问题，但他在偏微分方程中所考虑的方程并没有象在常微分方程中所考虑的方程那样有代表性。因此，后来又引进了模组的概念，柯西和稍后的С.Β.柯瓦列夫斯卡娅都用长函数法证明了模组柯西问题的解析解是惟一存在的。模的概念显然依赖于支柱。从而引入了特征的概念。应特别注意，有些组的特征表达式A能恒等于零，其中有些方程组是比较重要的，例如方程(2)就是这样的，广义相对论的基本方程组也是这样的。
在偏微分方程理论中，特征概念起着重要作用，所知特征的性质越多，相应的方程的研究的发展就越快。由于线性方程组和半线性方程组的特征只与(x1，x2，…，xm)有关，而与未知函数及其各阶导数无关，所以知道有关线性、半线性方程组（特别当系数是常数时）特征方程的信息较非线性方程组和拟线性方程组多得多，因为这时特征方程恒是一阶的，可以通过解一个常微分方程组而求得，从常微分方程关于解的含义来看，这个常系数的线性方程组的解就容易求得。在变系数线性方程中，n、m越大，特征就越复杂。方程的个数即未知函数的个数 n=1且阶数为 1时虽属浅显，却是一阶非线性偏微分方程柯西方法的基础。n=1，阶数为2时，特征表达式是
的二次型，代数学关于二次型已有特别多的结果，也是二阶线性偏微分方程发展比较成熟的一个原因。m＝2时特征表达式恒可分解为一定个数的线型的乘积。因此相应的方程组也发展较快。柯西-柯瓦列夫斯卡娅定理，并没有解决模方程组柯西问题的适定性问题，因为它只能证明解析解的惟一性，而并没有证明没有其他非解析解。20世纪初才由E.霍姆格伦在方程是非重特征的、系数是解析的、支柱是解析的而非特征的条件下，证明了解的惟一性。阿达马指出，只要能在方程是非重特征的、系数是非解析的、支柱是非特征的条件下证明霍姆格伦定理，则该定理在方程是非重特征的、非线性的、非解析的、支柱是非特征的条件下仍是正确的。至于连续依赖性则并不成立，阿达马的著名例子
就说明这个问题。阿达马分析了他以前和当时的有关线性二阶偏微分方程的工作，紧紧抓住“形式相似的方程却有迥然不同的适定问题”这个矛盾，反复论证，终于发现了长期未被注意的事实，即柯西-柯瓦列夫斯卡娅定理在方程、支柱和数据有一非解析时是不真的。例如Δu=0在支柱z=0的柯西问题在数据不都是解析时未必是有解的。诚然，双侧的解（即z≤0和z≥0时都存在的解）不存在，因为根据杜恩定理，若存在，则两个数据必然都是解析的。单侧的解也不存在，因为否则用照像法(实际上是一种解析开拓)，则双侧解也将存在，但解析方程
，解析支柱 t=0、非解析数据的柯西问题却是实际中提出的，理论证明是适定的。那么，哪一类方程应提柯西问题，哪一类方程应提狄利克雷型问题？物理学自然地，并基本地回答了这个问题。对刻画平衡和小运动的方程Δu=0，物理学提出了狄利克雷型问题；对刻画波的传递和大型运动的方程的
，对刻画不可逆现象的热导方程
，物理学提出了初值问题和混合问题；理论上也证明了这些定解问题都是适定的。但必需有数学的判别，才能彻底解决分类问题，即对一般的线性二阶偏微分方程
的分型问题。这里Aik、Bi、C 和ƒ 都是x1，x2，…，xm的已给解析函数，并有Aik＝Aki 。这个方程的特征表达式是
，这是一个只和原方程二阶项有关的
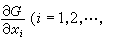m)的二次型。数学家早就知道二次型可以分为正（或负）定型、不定型和退缩型等类。特征表达式A为正（或负）定型的（ε）称为椭圆型方程，A为不定型的（ε）称为双曲型方程，A为退缩型的(ε)称为退缩型方程，其中有一种A可化为(m－1)个同号平方项的则称为抛物型方程。因之，Δu=0就是椭圆型方程，
就是双曲型方程，而 
则是抛物型方程。型不同，当然所提的定解问题也应不同。那么不同型方程有没有共性呢？阿达马提出了基本解。这不仅是他对前人工作的总结，而且从他本人以前的成就也必然得到这个重要概念。有了基本解，模双曲型方程的柯西问题的解，只要支柱是空向的，已给数据适当正规，就可以用一个发散积分的有限部分来表示；椭圆型方程就可以形成势代表解，并通过这个势满足的弗雷德霍尔姆型积分方程求得狄里克雷问题的解。间接地求抛物型方程的基本解的步骤也是阿达马提出来的。他有一句名言：“所有线性偏微分方程问题应该并且可以用基本解来解决。”
在V.沃尔泰拉暗示下，G.F.特里科米进行了混合型方程的所谓特里科米问题的研究。所谓混合型方程，是指在蜕型线L一侧是椭圆型，在另一侧是双曲型的方程；1927年特里科米证明了解的存在性。虽然苏联学者C.A.洽普雷金在V.沃尔泰拉之前已在射流理论中提出更一般的混合型方程即洽普雷金方程，但只有在40年代由于超音速飞机的制造，在跨音速气动力学中这类方程才大受重视。M.H.普罗特尔证明了洽普雷金方程特里科米问题的解的惟一性，苏联学者A.B.比察泽也在这方面做了大量有意义的工作。由于渗流的研究，促进了拟线性退缩抛物型方程的研究发展，苏联学者为此作出了贡献。
早期由于外弹道学的需要，以及40年代由于高速气动力学研究激波的需要，拟线性一阶双曲组的间断解的研究更得到了重大发展，苏联和美国学者作出了贡献。泛函分析和偏微分方程间的相互联系，相互促进发展，首先应归功于法、波、苏等国学者的努力。
中华人民共和国建立后，微分方程得到了重视和发展。培养了许多优秀的微分方程的工作者，在常微分方程稳定性、极限环、结构稳定性等方面做出了很多有水平的结果；在偏微分方程混合型刻画渗流问题的拟线性退缩抛物型、椭圆组和拟线性双曲组的间断解等方面做出了很多有水平的结果。
参考书目
J.Hadamard，Le Probléme de cauchy et les Equations aux Dérivées partielles Lineairs Hyperboliques，Hermann，Paris，1932.
J.Hadamard，la Theorie des Equatiens aux Dérivées partielles， Editions des Sciences，Beijing，1964.