数论(卷名:数学)
theory of number
研究数的规律,特别是研究整数性质的数学分支。它与几何学一样,既是最古老的数学分支,又是始终活跃着的数学研究领域。从方法上讲,数论可分成初等数论、解析数论与代数数论。
自然数分成1、素数和复合数。刻画自然数的基本规律,早在公元前4世纪就为欧几里得所证明,即每个复合数都可以惟一地表成素数的乘积。这又称为算术基本定理。素数分布是数论最早研究的课题之一,欧几里得证明过素数有无穷多。他还给出求两个自然数的最大公约数的算法,即所谓欧几里得算法。大约在公元前250年,埃拉托斯特尼发明一种筛法,可求出不超过某个自然数N的全部素数。后来的素数表都是根据这一方法略加改变而得出来的。
数论研究不定方程的求解问题。大约在公元 250年,丢番图研究过这种方程,故又称丢番图方程。最简单的不定方程为一次方程αx+by=1,此处α、b为整数,且互素即(α,b)=1。借助于欧几里得算法,可以求出它的解。如果整数α、b用正整数m除后,有相同的余数,就称α与b关于模m同余,记为α呏b(modm)。以x为变数的同余方程αx呏с(modm)(x=1,2,…,m),等价于求解一次不定方程αx+my=с,此处0<x≤m。同余方程即某些不定方程。中国古代即有关于不定方程的研究记载,如5世纪的《张丘建算经》中的“百鸡问题”及《孙子算经》中的“物不知其数”都属于一次不定方程问题。又如公元前1100年商高曾给出方程x2+y2=z2的一组解x=3,y=4,z=5。不定方程式论虽有长久的发展,但完满解决的问题并不多,如著名的费马猜想,即当整数n≥3时,方程xn+yn=zn没有正整数解,就是至今仍未解决的难题。最近,利用代数几何的成就,G.法尔廷斯出色地证明了,当n固定时,这一方程只有有限多个两两互素的正整数解。
研究将整数表为某种整数之和的问题,这一数论分支称为堆垒数论。例如,研究将整数表为正整数的k次方幂之和的种种问题,都属于华林问题范畴。又如,每一不小于4的偶数恒可以表为两个素数之和,就是尚未解决的哥德巴赫猜想。
定义于自然数集上的函数,称为数论函数。例如,欧拉函数φ(n),表示不超过n且与n互素的整数个数。σλ(n)表示n的因数的λ次方幂之和,特别地,σ0(n)=d(n)表示n的因数个数,以及r(n)表示不定方程n=x2+y2的解的个数,等等。
研究数论函数的性质,也是数论的一个重要课题。例如,
 可以分别用圆ξ2+η2≤x与区域ξη≤x,ξ≥1,η≤1的面积来作渐近计算,这种渐近计算的误差估计,就是著名的高斯圆问题与狄利克雷除数问题。它们的误差皆不超过
可以分别用圆ξ2+η2≤x与区域ξη≤x,ξ≥1,η≤1的面积来作渐近计算,这种渐近计算的误差估计,就是著名的高斯圆问题与狄利克雷除数问题。它们的误差皆不超过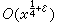 的猜想,也是一个未解决的难题。此处ε为任意正数。
的猜想,也是一个未解决的难题。此处ε为任意正数。对于任何实数α,如何构造有理数h/k(k>0)来逼近α? P.G.L.狄利克雷曾证明过,对于任意实数α及K>1,皆存在整数h、k使0<k<K及|α-h/k|≤1/kK。可以用连分数方法来构造h/k。将α展成连分数α=[α0,α1,…]。取h/k为α 的渐近分数,即h/k=[α0,α1,…,αn]即可。在5世纪时,中国的何承天与祖冲之就曾分别建议用22/7(约率)与355/113(密率)来近似表示π值。这两个数都是π的渐近分数。
有理逼近的研究与丢番图方程的研究是密切相关的,故又称为丢番图逼近。研究实数的种种有理逼近问题,是数论研究的一个重要课题。
数的几何学是用几何方法研究某些数论问题的一个数论分支。特别是种种丢番图逼近问题,例如,可以证明平面上以原点为对称中心的凸域,若其面积大于4,则必含有一个非原点的整点(闵科夫斯基定理)。由此可以立即推出上述狄利克雷关于实数的有理逼近定理。
特殊类型的数,是数论最早研究的对象之一。例如,形如Fn=22n+1的数,称为费马数。当n=0,1,2,3,4时,Fn都表示素数。P.de费马猜测Fn都表示素数,但L.欧拉证明了641|F5,所以费马的猜想被否定了。形如Mp=2p-1(p为素数)的素数,称为梅森素数。是否有无穷多个梅森素数?乃是没有解决的问题。迄今只知道28个梅森素数,其最大者为M86243,也是至今所知的最大素数。适合于σ1(n)=2n的整数,称为完全数。可以证明,偶完全数与梅森素数是一一对应的,故迄今共知道28个偶完全数。是否有奇完全数,是未解决之难题。
整数系数的代数方程的根,称为代数数;其他的复数则称为超越数。超越数也是数论较早研究的课题。例如,用初等方法可以证明e与π是超越数,运用复变函数论还可以证明
 等都是超越数。但欧拉常数与e+π是否为超越数,都是迄今尚未解决的难题。
等都是超越数。但欧拉常数与e+π是否为超越数,都是迄今尚未解决的难题。一般说来,用算术推导方法来论证数论命题的分支称为初等数论。而解析数论则是把一个算术问题化为一个分析问题,然后用分析的成果与方法来处理,从而导出算术的结果。当然,得到的常常是渐近性质的结果。如果在推导过程中,不用到单复变函数论中的柯西定理或同样深度的分析工具,仅仅只用到普通的数列求极限等等,则称为解析数论的初等方法。
解析数论开始于欧拉的一些研究,其中之一为关于素数有无穷多的证明。假定素数个数有限,则
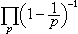 为有限数,此处p过所有素数,但
为有限数,此处p过所有素数,但 是发散的,故得矛盾。命π(x)表示不超过x的素数个数,则素数有无穷多可以表示为π(x)→∞。关于π(x)的研究是素数论的中心问题。首先是∏.Л.切比雪夫用初等方法证明了
是发散的,故得矛盾。命π(x)表示不超过x的素数个数,则素数有无穷多可以表示为π(x)→∞。关于π(x)的研究是素数论的中心问题。首先是∏.Л.切比雪夫用初等方法证明了 ,此处α=0.92129,尽管α的数值不断地被以后的数学家所改进,但并不能够证明素数定理,即
,此处α=0.92129,尽管α的数值不断地被以后的数学家所改进,但并不能够证明素数定理,即 的极限为1。
的极限为1。首先是(G.F.)B.黎曼确定了π(x)与他所引进的复变函数
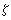 (s)(s=σ+it)之间的联系。当σ>1时,
(s)(s=σ+it)之间的联系。当σ>1时,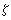 (s)由级数
(s)由级数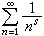 来定义,当σ≤1时,可以由解析开拓来定义。除s=1为
来定义,当σ≤1时,可以由解析开拓来定义。除s=1为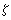 (s)的一次极外,
(s)的一次极外,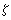 (s)在s平面上是正则的。黎曼猜想是说,在带状区域0≤σ≤1中,
(s)在s平面上是正则的。黎曼猜想是说,在带状区域0≤σ≤1中,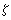 (s)的零点都位于直线σ=1/2上面。这一著名猜想是一个纯分析问题,但它与π(x)有密切关系,可以证明它等价于π(x)的极为精密的表达公式:
(s)的零点都位于直线σ=1/2上面。这一著名猜想是一个纯分析问题,但它与π(x)有密切关系,可以证明它等价于π(x)的极为精密的表达公式: ,此处
,此处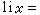
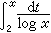 ,黎曼猜想离解决还相差很远。到目前为止,关于 π(x)最精密的估计是И.М.维诺格拉多夫与Η.М.科罗博夫证明得到的π(x)=lix+O(x exp(-(logx)0.6-
,黎曼猜想离解决还相差很远。到目前为止,关于 π(x)最精密的估计是И.М.维诺格拉多夫与Η.М.科罗博夫证明得到的π(x)=lix+O(x exp(-(logx)0.6- )),此处ε为任意正数。这是从
)),此处ε为任意正数。这是从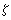 (x)的零点分布的结果中推导出来的。
(x)的零点分布的结果中推导出来的。有一系列重要的数论问题,特别是与素数有关的问题的完满解决,都关联着黎曼猜想及类似猜想的解决。例如,相邻素数之差pn+1-pn的估计问题,此处pn表示第n个素数。又如,算术级数 kn+l(n=1,2,…)中最小素数p(k,l)的估计问题,此处(k,l)=1。
命2|n及r2(n)表示方程n=p+p′的解p、p′的个数,此处p、p′为素数。命
 。由于
。由于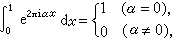 所以
所以 。命rs,k(n)表示方程 n=
。命rs,k(n)表示方程 n=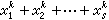 的解的个数,此处xj(1≤i≤s)均取正整数。又命
的解的个数,此处xj(1≤i≤s)均取正整数。又命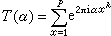 ,此处
,此处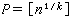 ,则
,则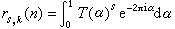 。
。将[0,1]分成优弧M与劣弧m。粗略地说,M为包含较小分母的分数的小区间所组成,[0,1]的其余部分为劣弧m。由于 r2(n)与rs,k(n)的积分表达式中在优弧部分的积分可以估计出来,所以它们的研究均归结为劣弧上的积分的研究。这就是G.H.哈代与J.E.李特尔伍德的圆法。
劣弧上积分的估计归结为在劣弧上指数和S(α)与T(α)的估计。这样一来,很多著名的数论问题(如上述的哥德巴赫问题与华林问题)都化为纯分析问题,即指数和的估计问题。
这种和的研究起源颇早,最初是C.F.高斯研究了形如S
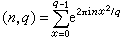 的指数和,此处(n,q)=1,他并证明了
的指数和,此处(n,q)=1,他并证明了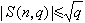 。将x2推广到一般的整系数多项式
。将x2推广到一般的整系数多项式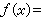
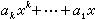 ,其中 (αk,…,α1,q)=1,这一历史难题是华罗庚解决的。命
,其中 (αk,…,α1,q)=1,这一历史难题是华罗庚解决的。命 ,华罗庚证明了
,华罗庚证明了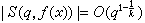 ,其中
,其中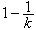 是最佳可能的。特别当q=p为素数时,由A.韦伊证明的有限域上类似的黎曼猜想可以推出
是最佳可能的。特别当q=p为素数时,由A.韦伊证明的有限域上类似的黎曼猜想可以推出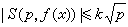 。韦伊证明了类似的黎曼猜想是基于他对代数几何学的深刻研究。这一结果最近已由C.A.斯捷潘诺夫、W.M.施密特和E.邦别里用分析方法加以证明。用代数几何学的积累,P.德利涅更证明了高维代数函数体上的类似黎曼猜想,由此可得到p 的多重完整三角和的精确估计。当ƒ(x)的系数为实数,这种广泛的指数和的研究是(C.H.)H.外尔开始的,所以又称这种和为外尔和。维诺格拉多夫创立了新的估计外尔和的精密方法,还创立了估计以素数为变数的指数和的方法。从而,关于哥德巴赫猜想,他用圆法证明了每个充分大的奇数都是三个素数之和;关于华林问题他证明了当s≥s0~2klogk时,每个充分大的整数都是s个正整数的 k次方幂之和。将华林问题与哥德巴赫问题结合起来,可以研究将整数n表为
。韦伊证明了类似的黎曼猜想是基于他对代数几何学的深刻研究。这一结果最近已由C.A.斯捷潘诺夫、W.M.施密特和E.邦别里用分析方法加以证明。用代数几何学的积累,P.德利涅更证明了高维代数函数体上的类似黎曼猜想,由此可得到p 的多重完整三角和的精确估计。当ƒ(x)的系数为实数,这种广泛的指数和的研究是(C.H.)H.外尔开始的,所以又称这种和为外尔和。维诺格拉多夫创立了新的估计外尔和的精密方法,还创立了估计以素数为变数的指数和的方法。从而,关于哥德巴赫猜想,他用圆法证明了每个充分大的奇数都是三个素数之和;关于华林问题他证明了当s≥s0~2klogk时,每个充分大的整数都是s个正整数的 k次方幂之和。将华林问题与哥德巴赫问题结合起来,可以研究将整数n表为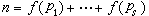 的问题,此处ƒ(x)为给定的k次整值多项式,pj(1≤i≤s)为素数。华罗庚对这一问题进行了系统的研究,除个别结果外,关于华林问题的结果,都可以推广到这个问题。
的问题,此处ƒ(x)为给定的k次整值多项式,pj(1≤i≤s)为素数。华罗庚对这一问题进行了系统的研究,除个别结果外,关于华林问题的结果,都可以推广到这个问题。另一个研究哥德巴赫猜想的方法是埃拉托斯特尼筛法的改进,这一方法的研究是V.布龙开始的。用这一方法,目前所得到的最佳结果是陈景润证明的,即每个充分大的偶数都是一个素数及一个不超过 2个素数的乘积之和。
由π(x)的研究可以看出,不同深度的方法得出了不同深度的结果。还可以举整数分拆问题为例。命p(n)表示将n分拆为整数和的方法数。用简单的算术方法可以得出p(n)最粗略的估计,
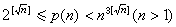 。用初等的分析方法可以证明
。用初等的分析方法可以证明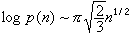 。用所谓的陶伯型定理就可以得出p(n)的渐近表达式。利用模形式论的结果及解析数论方法还可以求出p(n)的展开式。在逐步求精的方法中,容易看出各种不同方法之精度。
。用所谓的陶伯型定理就可以得出p(n)的渐近表达式。利用模形式论的结果及解析数论方法还可以求出p(n)的展开式。在逐步求精的方法中,容易看出各种不同方法之精度。另一方面,虽然有的问题已经由分析方法所解决,但是寻求一个算术的解决方法或较初等的分析解决方法,仍是很重要的事。例如,寻求素数定理的初等分析证明,即不依赖于ξ(s)零点分布成果的证明,是素数论中历时很久的问题之一。这一证明是由A.赛尔伯格与P.爱尔特希得到的。又如,R.特艾德曼用盖尔丰德-贝克方法基本解决了卡塔朗猜想,即方程xm=yn+1的整数解适合于|xm|<с,此处с是一个绝对常数。在此之前,柯召曾用初等方法证明,方程x2=yn+1只有整数解x=±3,y=2,n=3。
正因为数论问题很具体与特殊,所以在数论中发展起来的各种方法常常是很有用的。例如,指数和的估计方法与筛法在理论物理学、概率统计和组合数学中,都有重要的应用。
首项系数为1的整系数方程的根,称为代数整数。例如,普通整数,
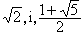 等都是代数整数。代数数论就是研究代数整数集合。代数整数集合是比普通整数集合更广泛的集合。
等都是代数整数。代数数论就是研究代数整数集合。代数整数集合是比普通整数集合更广泛的集合。在研究代数数论时,首先要引入代数数域的概念。所谓数域即加、减、乘、除运算自封的某复数的集合,例如有理数的全体Q构成一个域。Q添加一个代数数α,即得代数数域Q(α)。Q(α)中的代数整数的全体R,关于加、减、乘(除法除外)自封,构成一个环。算术基本定理对于一般代数整数是不成立的,例如,对于任何正整数n皆有
 。这建议人们仅考虑一个代数数域,即使如此,算术基本定理也可能不成立,例如,对于域
。这建议人们仅考虑一个代数数域,即使如此,算术基本定理也可能不成立,例如,对于域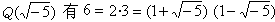 。在引入“理想数”概念之后,就可得惟一因子分解定理。所谓理想数是R的子集A,关于加、减自封,且R的元素乘以A的元素仍属于A。例如,R的一个元素x生成的集合xR即为一个理想数,这种理想数称为主理想数。可以定义理想数之间的乘法及素理想数,并可以证明算术基本定理对于理想数是成立的。
。在引入“理想数”概念之后,就可得惟一因子分解定理。所谓理想数是R的子集A,关于加、减自封,且R的元素乘以A的元素仍属于A。例如,R的一个元素x生成的集合xR即为一个理想数,这种理想数称为主理想数。可以定义理想数之间的乘法及素理想数,并可以证明算术基本定理对于理想数是成立的。在代数数域Q(α)中存在一组代数整数
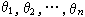 使R中任何元素u皆可以惟一表成
使R中任何元素u皆可以惟一表成 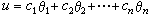 ,此处сj(1≤i≤m)为普通整数。
,此处сj(1≤i≤m)为普通整数。 称为Q(α)的整底。
称为Q(α)的整底。如果u与1/u都属于R,则称u为Q(α)的单位,除1的单位根外,R中常常还有其他单位。命α的定义方程有r1个根,r2对复根,又置r=r1+r2-1,则P.G.L.狄利克雷证明了在R中存在r个单位η1,η2,…,ηr使R中任何单位ε都可以惟一地表成
 ,此处ξ为单位根,而αj(1≤i≤r)均为普通整数。η1,η2,…,ηn称为Q(α)的基本单位组。
,此处ξ为单位根,而αj(1≤i≤r)均为普通整数。η1,η2,…,ηn称为Q(α)的基本单位组。还可以定义分数理想,即理想中含有非代数整数之元素。这些理想构成一个群。它关于主理想构成的子群的商群叫做类群。H.闵科夫斯基证明了类群是有限群。类群的元素个数称为代数数域的类数。类数为 1的代数数域中,代数整数有惟一因子分解定理。一般代数数域的类数是很难具体算出来的。对于虚二次域
 ,H.M.斯塔尔克与 A.贝克证明了,只有当m=1,2,3, 7,11,19,43,67与163时,
,H.M.斯塔尔克与 A.贝克证明了,只有当m=1,2,3, 7,11,19,43,67与163时, 的类数为1,C.F.高斯曾经猜测有无穷多个实二次域有类数1,这是尚未解决的难题。
的类数为1,C.F.高斯曾经猜测有无穷多个实二次域有类数1,这是尚未解决的难题。研究两个代数数域F与L,此处L为F的代数扩张。有一种代数数域特别重要,即L关于F的维数等于F的类数,而且F的任何理想在L中都是主理想,则L称为F的类域。类域论的研究是代数数论的一个重要课题。
代数数论的重要,不仅在于它是为弄清普通整数的某些规律所不可少的,而且在于它的成果几乎可以用到每一个数学领域中去。
近30年来,电子数字计算机的产生与发展给科学技术带来了无比巨大而深刻的变革。这使数论有了非常广阔的直接应用途径。众所周知,无论什么问题必需离散化之后才能在计算机上进行数值计算,所以离散数学日益显得重要,而离散数学的基础之一就是数论。例如,近20年发展起来的高维数值积分的数论网格法的研究中,数论的成果曾被广泛运用。一致分布理论、指数和估计,经典代数数论都被用到,甚至丢番图逼近论中施密特关于代数数的联立有理逼近定理也被用到,在华罗庚、王元的《高维数值积分的数论网格法》一书中有详尽的论述。在编码和数字信号处理问题中,数论也有很重要的应用。随着科学的发展,数论除其在纯粹数学中的基础性质外,已日益展现出直接应用的途径。这是近30年的事。
数论在中国古代有着悠久的研究历史。数论的研究也是中国近代数学最早开拓的数学研究领域之一。杨武之首先将近代数论引入中国。华罗庚、柯召、闵嗣鹤等是这一领域的研究在中国的创始人,特别是华罗庚在解析数论方面的卓越成就,在国际上有广泛深入的影响,在他领导下,培养出一批优秀的中国数论学家。
参考书目
L.E.Dickson,History of the Theory of Numbers,Vol.1~3, Carnagie Institute, 1919, 1920,1923.
华罗庚著:《数论导引》,科学出版社,北京,1957。