多面体群(卷名：数学)
polyhedral group
保持正多面体在空间占有位置不变的一切运动所成的群。一多面体在空间运动，其运动前后占有同一个空间位置，一切这样的运动的集合
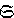，对于以两个这样的运动相继施行作为乘法构成群，称为多面体群。由几何学可知，正多面体只有5种，即正四面体、正六面体、正八面体、正十二面体、正二十面体。于是有正四面体群、正六（八）面体群、正十二（二十）面体群等三种群。在正四面体A-BCD中，以其正三角形BCD的中心O1与A点连结的直线AO1为轴，如图1
，将正四面体A-BCD 按反时针方向绕 AO1轴作角度为2π/3与4π/3的旋转。显然，这两个旋转运动分别对应于置换(BCD)与(BDC)，且使正四面体在其运动前后占有同一空间位置。仿此，连结 B点与正三角形ACD的中心O2的直线BO2为轴作角度为2π/3 与 4π/3的旋转，这两个旋转运动分别对应于置换(ACD)与(ADC)，并使正四面体在运动前后占有同一空间位置。同理，与置换(ABD)及(ADB)，(ABC)及(ACB)所对应的旋转，也使正四面体在运动前后占有同一空间位置。综上所述共有8个三项循环：(BCD)，(BDC)，(ACD)，(ADC)，(ABD)，(ADB)，(ABC)，(ACB)。它们分别对应的旋转都是使正四面体占有同一空间位置的运动。再以正四面体A-BCD的3对对边之中点联线为旋转轴， 作角度为π的3个旋转，它们分别对应于置换(AB)(CD)，(AC)(BD)，(AD)(BC)，并使正四面体占有同一空间位置。以I表示旋转角为0的旋转即不动旋转，显然，I是使正四面体占有同一空间位置的运动。总计共得12个旋转运动。除此之外再没有其他运动可保持正四面体占有空间位置不变。这样的12个运动构成群，称为正四面体群。它与4个文字A、B、C、D上的四次交错群
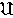4同构，因此，四次交错群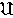4又称为正四面体群。正八面体A-BCDE-F，如图2a
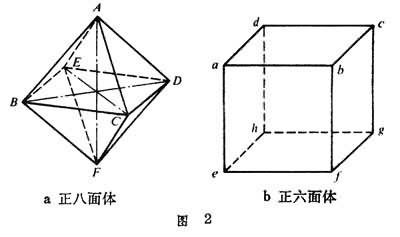，其各个面都是正三角形，顺次联结各面的中心α，b，с，d，e，ƒ，g，h即得一个正六面体αbсd-eƒgh，如图2b。对于正八面体A-BCDE-F分别以其 3条对角线AF，BD，CE为旋转轴，作π/2，π，3π/2的旋转，共有9个旋转运动。它们都能使正八面体占有同一空间位置，同时使正六面体也占有同一空间位置。以正八面体的4对对面的中心连线为旋转轴，分别作π/3、2π/3的旋转，共有8个这样的运动。它们使正八面体，也使正六面体不变更所占的空间位置。再以正八面体的6对两平行棱的中点联线为轴作角度为π的旋转，共有6个旋转运动。它们使正八面体，并因之使正六面体不变更占有的空间位置。加上不动旋转I，于是，使正八面体或正六面体不变更占有的空间位置的旋转运动，总计有24个，且只有这24个。这样的24个运动构成群，称为正八面体群或正六面体群。它与四次对称群
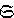4同构，所以正八面体群与正六面体群是一致的，都是 4次对称群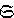4。 有时把四次对称群称为正八面体群或正六面体群。由于正十二面体的各面之中心的连线，可勾画出正二十面体（图3
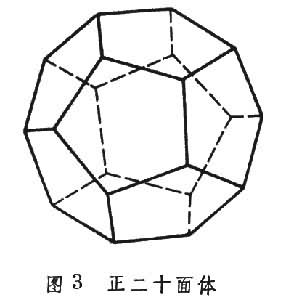）。因此，正十二面体群与正二十面体群是一致的。以正十二面体的 6对相对面的中心连线为轴作2π/5，4π/5，6π/5，8π/5的旋转，这样的旋转共有24个。以10对相对顶点的连线为轴作 2π/3、4π/3的旋转，这样的旋转共有20个。以15对相对对边的中心连线为轴作π的旋转， 这样的旋转共有15个。不动旋转I一个。于是，使正十二面体或正二十面体不变更占有的空间位置的旋转共有60个，且只有这60个。这样的60个旋转构成群，称为正十二面体群或正二十面体群。它与5次交错群
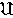5同构。自然界中的晶体都呈规则的多面体外形，且同一种晶体物质总是结晶成相同的形状，晶体还具有明显的各向异性。这些自然现象都可以用上述群论方法来研究。晶体的结构是其原子按一定方式相互连结的空间点阵，称为晶格。在这种点阵中可找到最基本的单位，称为晶胞。整个点阵相当于晶胞按一定规则的排列。晶格具有上述五种正多面体或其他几何体形状。例如食盐NaCl晶体的晶格就是正六面体形，如图4
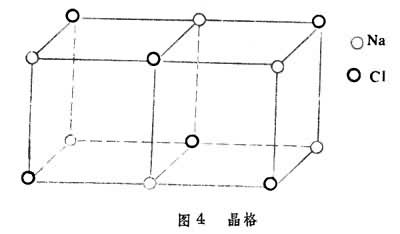。研究某种晶体的空间点阵时，有一些变换使空间点阵不变，这些空间变换不仅是前面所提及的旋转运动，而且还包括平移、镜面反射等运动。所有这些空间变换的集合成为一个群，称为晶体的空间群或结晶群。它反映了晶体的内部结构和晶体的性质。结晶群中的所有平移的集合是一个正规子群，称为平移子群。结晶群对其平移子群的商群，是一个类似于前面提到的多面体群的空间变换群，它刻画了晶格以及晶体宏观外形的对称性质，称为晶体点群。
晶体点群共有 32 个，其中包括正四面体群和正六(八)面体群。这是一个不太复杂而很有意义的结果。要得到与这32个晶体点群相联系的所有结晶群就复杂一些。一般的，从一个晶体点群出发，会发现多个结晶群以其为商群。尽管如此，结晶群的总个数也是不很多的，共有230个。找出这230个结晶群，并证明除此之外没有其他的结晶群的工作，已在19世纪末由E.C.费德洛夫(1895)、A.舍福里斯(1896)和W.巴罗(1894)完成了。这一工作可以说是群论对其他自然科学的首次成功的重大应用，它也推动了群论本身的发展。
参考书目
A. Speiser，Die Theorie der Gruppen von Endlicher Ordrung，3rd ed.，Springer-Verlag，Berlin，1937.