巴拿赫空间(卷名：数学)
Banach space
一种赋有“长度”的线性空间，泛函分析研究的基本对象之一。数学分析各个分支的发展为巴拿赫空间理论的诞生提供了许多丰富而生动的素材。从K.（T.W.）外尔斯特拉斯以来，人们久已十分关心闭区间[α，b]上的连续函数以及它们的一致收敛性。甚至在19世纪末，G.阿斯科利就得到[α，b]上一族连续函数之列紧性的判断准则，后来十分成功地用于常微分方程和复变函数论中。1909年F.（F.）里斯给出C[0，1]上连续线性泛函的表达式，这是分析学历史上的重大事件。还有一个极重要的空间，那就是由所有在[0，1]上p次可勒贝格求和的函数构成的Lp空间(1<p<∞)。在1910～1917年，人们研究它的种种初等性质；其上连续线性泛函的表示，则照亮了通往对偶理论的道路。人们还把弗雷德霍姆积分方程理论推广到这种空间，并且引进全连续算子的概念。当然还该想到希尔伯特空间。正是基于这些具体的、生动的素材，S.巴拿赫与N.维纳相互独立地在1922年提出当今所谓巴拿赫空间的概念，并且在不到10年的时间内便发展成一部本身相当完美而又有着多方面应用的理论。
定义 对于实(或复)数域K上的线性空间X，若有从X到R的函数‖x‖使得：①‖x‖≥0，‖x‖=0必须且只须x=0，②对α ∈K，有‖αx‖=α‖x‖，③‖x+y‖≤‖x‖+‖y‖，则称X为线性赋范空间，而称‖x‖为范数。
显然，范数这概念是Rn中向量长度概念的推广。如同有理数系可完备化为实数系，任何线性赋范空间也可按照距离d(x，y)=‖x-y‖作为度量空间而完备化。
完备的赋范线性空间称为巴拿赫空间。例如，设Ω为紧豪斯多夫空间，令C(Ω)表示Ω上一切实(或复)值连续函数的全体，则C(Ω)关于范数
成为一个巴拿赫空间。再如，设(Ω，μ)是正测度空间，令Lp(Ω，μ)表示Ω上一切p（p≥1）次可求和函数的全体，则Lp(Ω，μ)关于范数
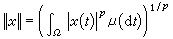成为一个巴拿赫空间。特别取Ω={1，2，3，…}，μ(n)＝1(当n＝1、2、3、…)则相应的Lp(Ω，μ)成为满足条件
的数列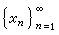
的全体，而相应的范数为
。一般记这个特殊的Lp（Ω，μ）为lp。还如，设(Ω，β，μ)是正测度空间，对Ω上可测的函数ƒ(t)，如果有正数α，使于Ω几乎处处有│ƒ｜(t)｜≤α，则称 ƒ(t)为本性有界的函数，而记上述诸α之下确界为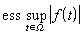
。令L∞(Ω)表示Ω上之本性有界函数的全体，则L∞(Ω)关于范数
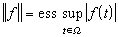成为一个巴拿赫空间。特别对Ω={1，2，3，…}而μ(n)=1(n=1，2，3，…)则相应的L∞(Ω)即有界数列
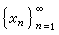的全体，而相应的范数为
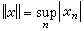。一般记这个特殊的L∞(Ω)为m。若
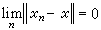，则称
强收敛于x，简写作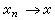
。基 作为完全就范直交函数系的推广，设
是巴拿赫空间X中的序列，如果对每个x ∈X 都恰有一数列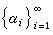
，使
，则称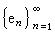
为X 的基，而称X为有基的空间。凡有基的空间一定是可分的，对于许多可分空间，人们具体地构造出它们的基。但是，是否每个可分的巴拿赫空间都有基的问题，直到1973年才由P.恩夫洛举出反例。确有可分而没有基的巴拿赫空间。对偶空间 设 ƒ(x)是从实(或复)域ƒ上赋范线性空间X到ƒ上的线性函数。若ƒ(x)还是连续的，则称ƒ(x)为连续线性泛函。一切如此的ƒ(x)按范数
构成的巴拿赫空间，便称为X的对偶空间(或共轭空间)并记作X*（或X′）。在许多数学分支中都会遇到对偶空间，例如矩量问题、偏微分方程理论等。一些物理系统的状态也常与适当空间上的线性泛函联系在一起。至于泛函分析本身，对偶空间也是极为重要的概念。通过X*，能更好地理解X。
里斯表现定理 设Ω是紧豪斯多夫空间，则于复的C(Ω)上的连续线性泛函ƒ(x)，便恰有Ω上的一个复正则波莱尔测度μ使
(1)并且‖ƒ‖=μ在Ω上的全变差 |μ|。许多人把这结果称作里斯表现定理。它是发展近代算子谱论的重要工具，还有着其他多方面的应用。这定理也可推广至局部紧豪斯多夫空间。许多测度来源于此定理。设Ω上所有复的正则波莱尔测度为m(Ω)，对每个μ∈m(Ω)，由(1)式定义的ƒ(x)是C(Ω)上的连续线性泛函，定义‖μ‖＝全变差|μ|，则C(Ω)*保范同构于m(Ω)。
例如，于正测度μ，有Lp(Ω，μ)(1<p<∞)上每个连续线性泛函ƒ(x)皆可表为
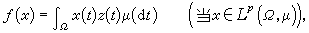(2)式中z(t)∈Lq(Ω，μ)，而
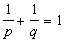，并且
。另一方面，由(2)式右端定义的泛函在[Lp(Ω，μ)]*中，总之[Lp(Ω，μ)]*保范同构于Lq(Ω，μ)。再如，于δ-有限的正测度μ，有L1(Ω，μ)上的连续线性泛函ƒ(x)可表为
(3)式中z(t)∈L∞(Ω，μ)，并且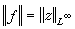
另一方面，由(3)定义的泛函在 [L1(Ω)]*中。总之，[L1(Ω，μ)]*保范同构于L∞(Ω，μ)。由于古典分析发展的要求，也因为巴拿赫空间理论本身的需要，于是人们研究X与X*之间的关系，这便是对偶理论。这理论的主要工具是哈恩－巴拿赫扩张定理:设M是线性赋范空间X的闭线性子空间，则①对M上的连续线性泛函g(x)，恒有ƒ(x)∈X*使ƒ(x)=g(x)，当x∈M，又‖ƒ‖=‖g‖(
);②对X中任给的x0≠0，恒有 ƒ(x)∈X* 使 ƒ(x0)=‖x0‖，‖ƒ‖=1，③对任意
，恒有ƒ(x)∈X*当x∈M使得ƒ(x)=0，ƒ(x0)=1，并且‖ƒ‖=1/d，这里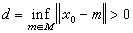
。设ƒ(x)∈X*，一般称点集H={x∈X;ƒ(x)＝常数C}为X中的闭超平面。设M是X的子空间，x0∈X，则称点集x0+M为X中的线性簇。这样，哈恩－巴拿赫定理便有如下的几何解释：若X中的线性簇m与非空的开凸集K不相交，则有闭超平面H使
而
。自反空间 对巴拿赫空间 X有对偶空间X*，而X*的对偶空间则记作X**，任给x0∈X，通过
（当x*∈X*）便确定一个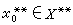
，并且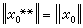
。这表明存在映射τ把X保范地嵌入到X**中。一般
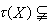X**。如果τ(X)＝X**，则称X为自反空间。典型的自反空间是Lp[0，1](1<p<∞)，但L1[0，1]与C[0，1]都不自反。弱收敛 无穷维巴拿赫空间的单位球是不可能按范数拓扑为紧的，因此许多有限维空间的命题都不能推广到一般巴拿赫空间。针对这一点，人们引进弱收敛的概念。对X 中
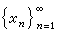与 x0，若于任何 x*∈X *都有
，则称
弱收敛于x0，记作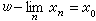
。埃伯莱因－什穆利扬定理 巴拿赫空间X是自反的；必须且只须 X中任何按范数有界的点列都含有弱收敛的子序列。
利用自反空间的这个拓扑性质，便能证明如下的结果：设J(x)是自反空间X之有界凸闭集C上弱下半连续的有界泛函，则J(x)在C上达到最小值。
应该指出，正是为着使得一些重要的命题得以成立，人们才引进种种类型的巴拿赫空间，自反空间就是一个鲜明的例子。再如与上述极值问题的惟一性有关，有所谓球状空间；与拉东-尼科迪姆定理相关，则有一致凸空间等等。
人们曾经长久地停留在序列弱收敛上。其实即使对于l2上的弱拓扑，只用序列弱收敛也是不行的。J.冯·诺伊曼首先看到这一点，并且在1930年就使用弱邻域概念。
X上使得一切x*∈X* 都连续的最弱的拓扑称为X上的弱拓扑。全体
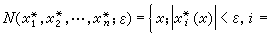
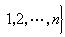，其中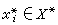
，ε>0，n=1，2，…构成X 在O点的一个弱邻域基。X*上使得一切
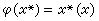，x∈X都连续的最弱的拓扑称为X*上的弱*拓扑。全体 
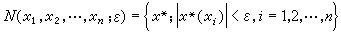，其中
，ε>0，n=1，2，…构成X *在O点的一个弱*邻域基。线性算子 设T是从实（或复）域F上的线性空间X中线性流形M到F上的线性空间Y的映射，如果
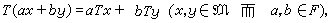则称T是线性算子，M为T的定义域，记作D(T)。特别当M=X 而Y为数域F 时，T 便称为X上的线性泛函。设X、Y都是赋范线性空间，x0∈D(T)，若对D(T)中任何收敛于x0的序列
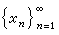都有 Txn→Tx0，则称T 在x0处连续。设D(T)=X， 则线性算子T 在X 上每点都连续必须且只须T是有界的， 即
。这时还称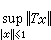
为T的范数，记作‖T‖。设X与Y都是数域F上的线性空间，A与B都是从X到Y的线性算子，对A与B可定义如下的运算:(A+B)x=Ax+Bx，(αA)x=α(Ax)，当x∈X，α∈F又定义(AB)x=A(Bx)，x∈X，当 A与B都是从X到X的线性算子时。若线性算子T是单射的，则将它的逆映射记作T-1，而Ix=x则称为单位算子或恒等算子。
设H为度量空间，
，对 x0 ∈E， 若有小球
，则称x0在E的内部。若点集S的闭包埅之内部是空的，则称S在H中无处稠密。若度量空间H中的点集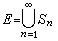
，而每个Sn皆在H中无处稠密，则称E为H中第一纲的点集。H中非第一纲的点集叫做第二纲的。显然全体有理数在实轴上便是第一纲的。可以这样想：第一纲的点集是比较稀疏的。贝尔纲定理 完备的度量空间必定是第二纲的。这是区间套定理的发展和提高，在证明许多存在定理时是很有用处的。在勒贝格关于奇异积分与O.特普利茨关于正则求和法以及哈恩关于插值理论等方面的研究之后，巴拿赫与H.斯坦豪斯在1927年给出共鸣定理。
共鸣定理 又称一致有界原理。设X是巴拿赫空间，Y是线性赋范空间，
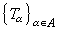是一族从X到Y的有界线性算子。如果
当x∈X，则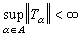
。这是有着多方面应用的重要定理，是纲定理的直接推论。和纲推理密切相关，还有极著名的开映射定理。开映射定理 设X与Y都是巴拿赫空间，若T是从X到Y的有界线性算子，且TX=Y，则T变X的开集为Y中的开集。这在有限维空间是平凡的，但在无限维空间却是极为深刻有力的工具。它有下列重要推论。
巴拿赫逆算子定理 设X与Y都是巴拿赫空间，若T是从X到Y的有界线性算子，且T是一对一的，又TX=Y，则T-1连续。
开映射定理还有一个关于闭算子的重要推论。设y=Tx是线性的，若从
恒有x0∈D(T)且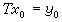
，则称T为闭算子。闭算子在应用上是非常重要的概念。表面上，闭性与连续性很相似，其实差异不小，因为连续性是从较少的假设xn→x0到更多的结论
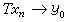且
。一般称X×Y中之G(T)={<x， Tx>；x∈D(T)}为 T的图像。易见T是闭算子，则G(T)按范数‖<x，y>‖=‖x‖+‖y‖是闭的点集。闭图像定理 设X与Y都是巴拿赫空间，若T是从X到Y的线性算子，则T是有界的必须且只须G(T)是闭的。
共轭算子 设X与Y都是巴拿赫空间。若线性算子T的定义域D(T)在X中稠密，而T 的值都在Y中，如果对
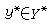有x*∈X*使当x∈D(T)时，y*(Tx)=x*(x)则x*由y*惟一确定，记作T′y*=x*，一般称T′为T的共轭算子或对偶算子。特别当T是从X到Y的有界线性算子时，则T′也是有界的，且‖T′‖=‖T‖。显然，共轭算子是转置矩阵的推广，所以它自然地在研究方程Tx=y时起着重要的作用。设A为巴拿赫空间X上的线性算子，称N(A)={x;Ax=0}为A的零空间，R(A)={y;y=Ax，x∈D(A)}为A的值域。从线性方程组的解，已经看到A与A′之值域与零空间的密切关系，后来在弗雷德霍姆理论中又再次看到这点。
对点集
，所谓M在X*中的零化子即
而于点集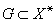
，则G在X中之零化子即
。设A为巴拿赫空间上有界线性算子，则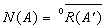
， 
，
， 
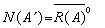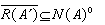。若又设X 自反，则
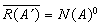。闭值域定理 设X与Y是巴拿赫空间，而T是从X到Y的闭线性算子，且
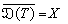，则下列命题等价：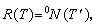
。参考书目
S.Banach，Théorie des Opérations Linéaires， Monografje Mathematyczne， Warsaw， 1932.
N.Dunford and J.T.Schwartz，Linear Operators， Part 1.General Theory，Interscience， New York， 1958.
A.E.Taylor and D.C.Lay，Introduction to functional Analysis， John Wiley & Sons， New York， 1979.