大气动力方程(卷名：大气科学 海洋科学 水文科学)
dynamic equations of atmospheric motion
描写大气运动和状态变化的方程。在大气动力学中，根据经典力学的牛顿运动定律，特别是牛顿第二运动定律，推导出大气运动方程；根据质量守恒定律，推导出大气连续方程；根据热力学第一定律得出热流量方程；再加上状态方程和水汽方程，就构成了描写大气运动和状态变化（包括水的相变）的动力方程组。这套方程组是研究大气的一切运动和现象的基础。
动 力 方 程 组
运动方程 在固定于地面的坐标中，对单位质量气块而言，由牛顿第二定律得大气运动方程的矢量形式为
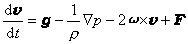式中v为风速矢量，t为时间，dv/dt为气块的加速度矢量；
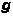为重力；
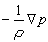为气压梯度力（ρ、p分别为空气的密度和气压）；ω为地球自转角速度矢量，
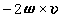为科里奥利力；F为粘性力，主要是湍流粘性力（见大气中的作用力）。连续方程 大气是具可压缩性的连续介质，由质量守恒定律可得：
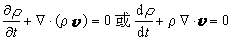
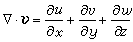称为三维速度散度，其中u、v、w分别是x、y、z方向的速度分量。
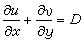为水平速度的散度，D>0，为水平辐散；D<0，为水平辐合。热流量方程 由热力学第一定律可推出热流量方程：
在运动过程中，如果大气不与外界交换热量，即Q=0，则热流量方程变为绝热方程：
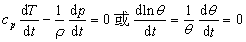
状态方程 均匀物质系统处于热力学平衡状态时，其体积、压强和温度间的关系式。在对流层和平流层的大气，可视为理想气体，其气压<p、气温T 和密度ρ 遵守理想气体状态方程
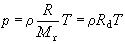
水汽方程 决定湿空气气块中的水汽含量变化的方程：
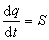
上面五个方程构成了描写大气运动的基本方程组，这是由V.皮耶克尼斯于1904年首先建立的。其中任一物理量A 的个别变化dA/dt，都可以表示为
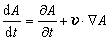式中дA/дt为 A 的局地变化项；v·墷A 为平流项，它又可分为水平平流
和铅直平流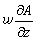
两个部分。平流变化代表某一气块的物理量A 在平流运动中不变时，它沿气流方向移到某地（或某高度）之后，使该地同一物理量所产生的变化。常 用 方 程
根据动力方程组，可以导出大气动力学中几个常用的方程。
涡度方程 速度场的旋度，在气象学中称为涡度。
三维涡度方程 将运动方程作旋度运算(即墷×)，就得到地球大气的三维涡度方程：
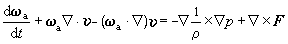式中ωa=ωr+2ω，为气块的绝对涡度。2ω为牵连涡度，是由于大气和地球一起旋转引起的；ωr= 墷×v=ξi +ηj+ζk ，为气块的相对涡度，其中i、j、k 为x、y、z方向的单位矢量，ξ、η、ζ分别为相对涡度在x、у、z方向上的分量：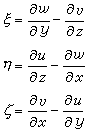
铅直涡度方程 研究大气的大尺度运动（水平尺度ι)的量级为103公里）时，由于它是准水平的运动，在这种情况下，可以得到一个铅直涡度方程，其形式为
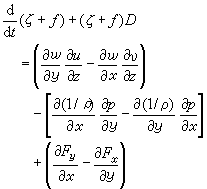式中x指向东，у 指向北，z 铅直向上；f为科里奥利参数，ζ+f =ζa是绝对涡度的铅直分量；Fx、Fy分别为粘性力在x、у方向的分量。铅直涡度方程右端第一项为涡管项；第二项为力管项；第三项为摩擦项。绝对涡度守恒 对于正压（见正压大气）无摩擦运动，铅直涡度方程化为
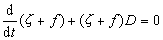
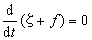
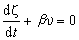
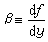，为罗斯比参数。铅直涡度ζ在天气实践中应用颇多，通常北半球气旋式流场，ζ>0；反气旋式流场，ζ<0（见大气波动）。在地转风的条件下，若用气压p 作铅直坐标，则ζ可以用重力位势Ф来表示（见大气运动的平衡状态）：
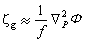
位势涡度方程 将运动方程、连续方程、热流量方程结合在一起，得位势涡度方程:
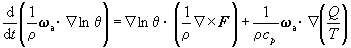
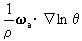为位势涡度。 位势涡度守恒定律 对于绝热无摩擦的大气运动，Q =0，F =0，则有：
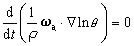它称为位势涡度守恒定律，是H.埃特尔在1942年发现的。对于大气大尺度水平运动来说，在气压坐标中有：
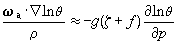因此位势涡度守恒定律可改写为
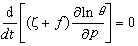用这公式表达的位势涡度守恒定律，是 C.-G.罗斯比在1940年发现的，它是大气大尺度运动在绝热、无摩擦和准地转条件下的综合定律。根据此定律，我们可以较方便地解释非绝热加热的铅直不均匀性对大气稳定度的影响，以及南北向大地形在形成长波槽中的作用。散度方程 对于大尺度运动，常用（水平）散度方程。它是由水平运动方程作水平散度运算而得，其形式为
式中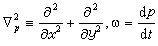
是气压坐标系中的铅直速度。 对于无摩擦的水平运动，散度方程化为
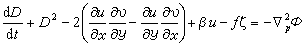
平衡方程 对于无摩擦、无辐散的水平大尺度运动，在气压坐标中，散度方程转化为平衡方程：
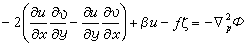式中所有对x和у的微商，都是指在气压坐标中的微商。因为它是在水平无辐散
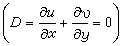的条件下得到的，故可以引入流函数ψ:
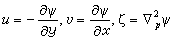这时，平衡方程又可表达为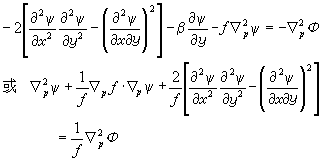
平衡方程给出了风场和气压场之间更普遍的关系。地转风的关系只是平衡方程在特定条件下的例子。对于分布均匀的圆形流线来说，在f为常数的情形下，平衡方程就表示了梯度风关系。
参考书目
J.PedloskyGeophysicalFluid Dynamics，Springer-Verlag，New York，1979.J.R.霍尔顿著，中国人民解放军空军气象学院训练部译：《动力气象学引论》，科学出版社，北京，1980。
J.R.Holton，AnIntroduction to Dynamic Meteoro-logy，2nd ed.，Academic Press，London，1979.