闭曲面的分类(卷名：数学)
classification of closed surfaces
关于空间的拓扑分类，这是一个既重要又有趣，然而也是非常难的问题，至今没有能完全解决。但限于闭曲面的情形，结果是非常完满的。它是数学中为数不多的几个完整的漂亮定理之一。
在众多的闭曲面中，球面显然是首先会被想到的，实际上，它可以作为构造其他的闭曲面的出发点。
为了从球面得到其他的闭曲面，先在球面上剪去几块，或者换一种说法，就是打些洞，然后再用适当的“补钉”将这些洞补上。当然，为了得到新的闭曲面，不能用刚剪下来的那种小圆片当“补钉”，而应换用其他类型的曲面。显然，如果用平环（如图1所示的阴影部分）
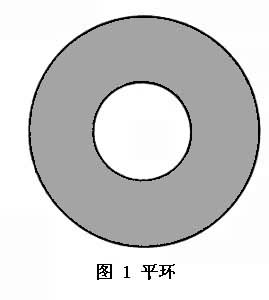
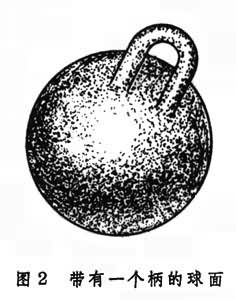作为“补钉”来补（平环的外圆周和洞的边缘粘合），那么球面上的洞补好了，而平环本身的洞（内圆周）仍空着。为了补这个新出现的洞，显然只要把它和球面上另一个洞的边缘粘合即可。这样，用平环（它拓扑等价于圆柱面）这种“补钉”来补洞，一次就可将两个洞补好。也就是说，把圆柱面的上端圆周和球面上的一个洞的边缘(也是一个圆周)粘合，而把下端圆周和球面上的另一个洞的边缘粘合。图2为用这种办法修补后得到的闭曲面。这种曲面由于像给球面安了个柄，故称它为带有一个柄的球面。显然，我们可以往球面上安任意多个柄，这些具有不同数目的柄的球面，构成不同胚的闭曲面的“一半”。在介绍另“一半”之前，应注意到以上的闭曲面都是双侧的，即其中一侧可以涂一种颜色，而另一侧则可涂另一种颜色。用平环这种“补钉”修补球面上的洞时，先是将外圆周和一个洞的边缘粘合，然后再将内圆周和另一个洞的边缘粘合。这样做的理由是因为最后要得到闭曲面。为了得到闭曲面，也可以直接将内圆周上的点，按粘合对径点(同一条直径上的两个端点)的方式把它封闭起来。这种先将内圆周沿对径点粘好的“补钉”，称为“交叉帽”，一个交叉帽可以补一个洞。带有任意多个交叉帽的球面，就构成另一半闭曲面。总而言之，任意一个闭曲面，它不是和一个安有若干个柄的球面同胚，就是和一个带有某些个交叉帽的球面同胚。
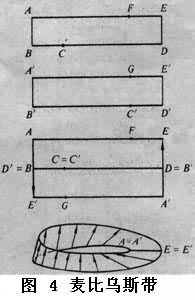
交叉帽是将平环的内圆周沿对径点粘合。现将平环沿AB和DE剪开（图3），得到ACDEF和A′B′C′D′E′G 两块（这里A剪开成A和A′，B、D、E，同此，但B和D是对径点应粘合，故B、B′，D、D′为同一点）。现将这两块沿BCD和D′C′B′粘合。如图4，所示，在长方形
中，两垂直边AE′和A′E沿标明方向粘合。这种将长方形的一对边，扭180°再粘合而得到的曲面叫做麦比乌斯带（见彩图）。
因此交叉帽就是麦比乌斯带。它除了只有一个边缘（平环的外圆周）这一特点外，还有另一个特点──单侧，即不能用两种不同的颜色来涂满两个侧面。因此带交叉帽的球面也是单侧的。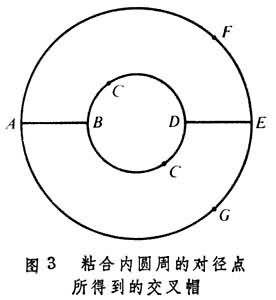
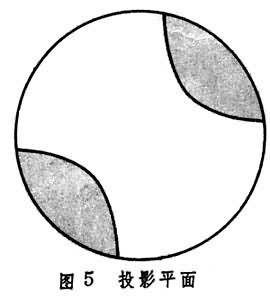
带一个交叉帽的球面，就是投影平面（投影平面就是将单位圆的对径点粘合而得，见图5。由于对径点粘合，故阴影部分同胚于有一个洞的球面，而余下部分为麦比乌斯带）；带两个交叉帽的球面，通常叫做单侧双环面或克莱因瓶（见图6及见彩图）。
单侧曲面画出来都是要自己和自己相交的。