速度(卷名：物理学)
velocity
描述动点在某一瞬时位置变化率的物理量，它是一个矢量，用
表示。点在直线运动中的速度 设动点在某一参照系中的轨迹是直线，令坐标轴Ox重合于轨迹直线（图1），于是，在每一时刻，点在轨迹上的位置M可用它的坐标x表示，点的直线运动方程为
x＝x(t)。如果已知函数x(t)，就可由运动方程确定点在任何一个时刻的位置。设点在时刻t和t′的位置分别为M和M′，相应的坐标为x和x′，Δx＝x'x 表示点在Δt＝t't这段时间内所走过的距离。比值
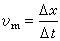表示点在Δt时间内位置的平均变化率，一般它并不表示点在瞬时t位置的变化率；但若Δt愈小，υm就愈能近似地表示点在瞬时t位置的变化率，所以
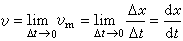称为点在时刻t的速度，简称速度。当v>0时，点沿Ox轴正方向运动；v<0时，则沿Ox轴的负方向运动。
点在曲线运动中的速度 设点在某一参照系（如直角坐标系Oxyz，图2）中的轨迹是一条空间曲线，点的运动方程可以表示为
r＝r(t)，式中r表示时刻t点在轨迹上的位置M的矢径，它是随时间而变化的。设在瞬时t′，点在轨迹上的位置为M′，矢径为r′，矢量 Δr＝r'r表示点在Δt时间内的位移矢量，于是
是点在曲线运动中瞬时t的速度，它是点的位置矢径对时间的一阶导数，它描述点的矢径的大小和方向的变化，是一矢量，其大小为dr/dt的模，其方向沿Δr的极限方向，也即沿瞬时t点在轨迹M点的切线方向（图2）。令υx、υy、υz和x、y、z分别表示点在时刻t的速度υ和矢径r在各坐标轴上的投影，则
即速度矢量 v在各坐标轴上的投影等于点的相应坐标对时间的一阶导数。于是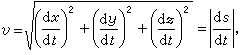
式中v是速度的模，称为速率，它总是一个正量；s表示由运动轨迹上的某定点 M0量起的至 M点的弧长。速度v的大小用υ表示，描述某瞬时点运动快慢的程度。速度v的方向可由矢量 v与各坐标轴夹角的方向余弦决定，即cos(v，i)＝υx/υ，cos(v，j)＝υy/υ，cos(v，k)＝υz/υ，式中i、j、k分别为x、y、z轴的单位矢量。
速度的合成 设点M相对某一参照系O′x′y′z′运动，而这个参照系（称为运动参照系）又相对另一个静止参照系 Oxyz 运动。这时，称点对于运动参照系的运动为相对运动；而称运动参照系对于静止参照系的运动为牵连运动；点对于静止参照系的运动为绝对运动或复合运动。点在相对运动和绝对运动中的速度分别称为相对速度和绝对速度，它们分别用vr和va表示。把点看成是和运动参照系相固连，随参照系运动而具有的速度称为牵连速度，用ve表示。这些速度之间的关系为
va＝vr+ve，即点的绝对速度 va是它的相对速度vr与牵连速度ve的矢量和，这就是速度的合成定理。
速度的量纲是LT-1，它的SI单位为m/s。