泰勒级数(卷名：数学)
Taylor series
解析函数的一类幂级数展开式。在圆|z－α|<R内解析的函数ƒ(z)可以展为以下形式的幂级数
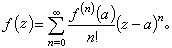(1)级数(1)称为函数ƒ(z)在点z=α的泰勒级数。当α=0时，称为马克劳林级数。设z是圆│
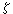-α│<R内的任意一点，作圆γ;|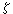-α|=r<R使得z位于γ的内部。根据柯西公式得到
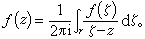(2)因为
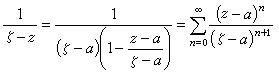，并且右边的级数在γ上一致收敛，所以将此式代入(2)式，逐项积分后就得到
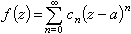， (3)式中
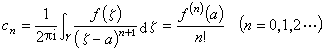。 (4)零点 若ƒ(α)=ƒ′(α)=…=ƒ(m-1)(α)=0，ƒ(m)(α)≠0，则称α是ƒ（z）的一个m级零点。特别地，若m=1，则称α是ƒ(z)的一个简单零点。
根据解析函数可以展为泰勒级数的上述事实，可以得到解析函数以下两个重要性质。
① 零点的孤立性 若ƒ(z)是域D内不恒为零的解析函数，则ƒ(z)在D内的零点是孤立的。也就是说，若ƒ(α)=0 (α∈D)，则存在α的一个邻域，使得ƒ(z)在该邻域内除α点外没有其他零点。
② 惟一性定理 设ƒ1(z)，ƒ2(z)是域D内的两个解析函数，若存在点集A嶅D，它有一个属于D的极限点α，且在A上ƒ1(z)=ƒ2(z)，则在D内ƒ1(z)=ƒ2(z)。惟一性定理可由零点孤立性推出。
柯西不等式 若函数 ƒ(z)在圆│z-α│<R内是解析的，且│ƒ(z)│≤M，则ƒ(z)在圆│z-α│<R内的泰勒级数
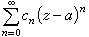的系数сn满足不等式
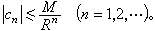(5)事实上，由(4)式得
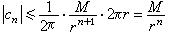，令r→R，就得到(5)式。刘维尔定理 若ƒ(z)是有穷复平面上的有界解析函数，则ƒ(z)必为常数。
事实上，这时(3)式在圆|z-α|<R内成立，R是任意正数，由柯西不等式立即推出сn＝0(n≥1)即ƒ(z)呏с0(常数)。