博弈论(卷名:政治学)
game theory
又称对策论。研究由一些带有相互竞争性质的主体所构成的体系的理论。它能以数字表示人的行为或为人的行为建立模式,研究对抗局势中最优的对抗策略和稳定局势,以及如何追求各方的最优策略和决定对策的结果,协助人们在一定规则范围内寻求最合理的行为方式。它曾被广泛运用于政治学、经济学、军事学、心理学等社会科学领域,特别是在国际政治学中被当作一种特殊的决策方法,成为指导国际冲突和对冲突结局作出估价的一种特殊手段。
博弈论最初是一门数学分支学科,起源于20世纪初。1921年,法国数学家┵.波莱尔研究了后来成为博弈论中重要内容的“有限最小最大战略”,但他否定了形成一般定理的可能性。1928年,美籍匈牙利数学家J.von诺伊曼证明了前人的假设,形成了诺伊曼“最小最大定理”。1944年,诺伊曼与O.莫根施特恩合著的《博弈论与经济行为》一书,提出了博弈论在经济活动中的运用问题,成为博弈论的奠基之作。以后,博弈论逐渐被引入政治学、军事学、心理学等领域。
博弈论的前提是,在冲突局势中,参加者一方的战略和决策取决于冲突局势中另一方的战略和决策,而且这种战略和决策处于参加者一方的控制之外。这种局势正如室内游戏中的情况,所以理论家把这种模型称为博弈论。博弈现象中存在 3个基本要素:①局中人,即一场竞争或斗争的参加者,他们各处于对抗局势对立面的一方。②策略,指局中人能采取的对付对手的一切行动。③赢得,即一局对策的得失。根据博弈现象的上述要素,可以把博弈论分为两种主要类型:①双方零和博弈。局中人为两个,其对策结果的赢得值代数和为零,如果一方的收益为 x,则另一方的收益为-x,一方所得为另一方所失,双方的利益直接冲突。学者们认为,在国际政治实践中,双方毫无共同利益的情形非常罕见,零和博弈论对国际政治的研究价值非常有限。②双方非零和博弈。两个局中人在任何局势下的赢得值的代数和不等于零,也不等于某个常数,即双方可能都得到某种利益,可能均受到某种程度的损失,也可能一方有得,一方有失,但得失绝对值并不相等。在非零和博弈中,参加各方既存在着共同利益,又是一种竞争关系。他们既可能采纳合作战略,也可能采取不合作战略。如一种被称为“囚犯的困境”的博弈模型:两个囚犯被分别告知,如果其中一个早一天交待,他就可以获释,并得到奖赏(假设赢得值为11),另一个囚犯则将被处死(赢得值为-20);如果他们同一天坦白,那么各判徒刑10年(赢得值为1);如果都不认罪,则都可获释,但没有奖赏(赢得值为10)。双方彼此隔离,无法传递信息,结果第二天都交待了罪行。假设两个囚犯A与B,A1、B1为各自拒不交待,A2、B2为各自交待,那么这种博弈模型可用图式表示:
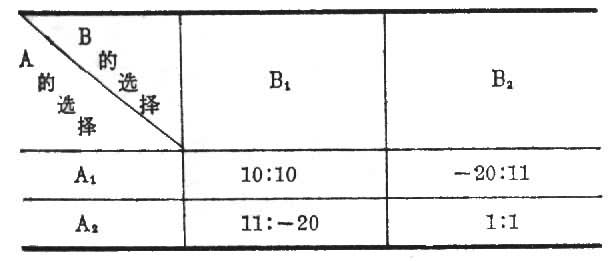
在这种对阵中,A1和B1是合作战略,A2和B2则是不合作战略。根据赢得数值,显然采取合作战略为上策,双方均可得到一定好处。但是,按照博弈逻辑,双方往往会选择不合作战略。
博弈论虽然作为一种在假设情况下分析人们行为的方法,能够帮助决策者在复杂的危机或竞争的情况下作出最佳的战略抉择。但政治、军事等领域,其变数、变量往往很难全部确定,故博弈论的运用有其局限性。