概率(卷名：数学)
probability
随机事件出现的可能性的量度。它是概率论最基本的概念。在一个特定的随机试验中，称每一可能出现的结果为一个基本事件，全体基本事件的集合称为基本空间。随机事件(简称事件)是由某些基本事件组成的，也就是基本空间的某些元素组成的集合（即基本空间的子集）。例如，在连续掷两次骰子的随机试验中，用m，n分别表示第一次和第二次掷出的点数，m，n可以取值1、2、3、4、5、6，每一 (m，n)表示一个基本事件，因而基本空间包含36个元素。“点数之和为2”是一事件，它是由一个基本事件(1，1)组成的，可用集合｛(1，1)｝表示；“点数之和为4”也是事件，它由(1，3)，(2，2)，(3，1)三个基本事件组成，可用集合｛(1，3)(3，1)(2，2)｝表示。如果把“点数之和为1”也看成事件，则它是一个不含任何基本事件的事件，称为不可能事件。常用Ω表示基本空间，ω 表示基本事件，空集符号═表示不可能事件。若A是一个事件，则“事件A不发生”也是一个事件，它由Ω中A以外的诸元素组成，记作Ac，称为A的对立事件。实际中要考察的各种各样的事件及其相互关系，正与基本空间Ω中元素所组成的各种子集及其相互关系相对应，因而概率论与集合论的语言有如表
中的对照，事件的关系可以表示如图1。在概率论中，并不总是把基本空间Ω的一切子集都当作事件。为了研究事件间的各种关系，记全体事件所构成的集类为F，它应具有以下性质：①Ω∈F；②若A∈F，则Ac∈F;③若A，B∈F；则A∪B∈F。这样的集类F称为域或代数。从这三条性质还可以推出：═=Ωc∈F;若A，B∈F，则A∩B=(Ac∪Bc)c∈F。
古典概率 古典概率讨论的对象局限于随机试验所有可能结果为有限个等可能的情形。这时基本空间Ω由有限个元素或基本事件组成，其个数记为n。域F由Ω的一切子集组成。若事件A包含m个基本事件，则定义A的概率P(A)=m/n，这就是P.-S.拉普拉斯的古典概率定义，或称之为概率的古典定义。
历史上有名的得分问题的解法是应用古典概率的一个典型例子：甲、乙二人各出同样的赌注，用掷硬币作为博弈手段。每掷一次，若正面朝上(+)，甲得1分，乙不得分；若反面朝上(－)，乙得1分，甲不得分。谁先得到事先约定的分数，就赢得全部赌注。当进行到甲还差2分，乙还差3分，就分别达到约定分数时，他们不愿继续赌下去，问这时如何公平分配赌注？显然，为确保能分出胜负，最多需要再掷 4次，共16种等可能的情形：{(+ + + +)， ( + + + -)， (+ + - +)， (+ + - - )，(+ - + +)，(+ - + -)，(- + + +)，(- + + -)，(- -- +)，(- - - -)，(+ - - +)，(- + - +)，(- - + +)，(+ - - -)，(- + - -)，(- - + -)｝。其中使甲获胜，即出现至少两个“+”的情形有11种，使乙获胜，即出现至少三个“－”的情形有5种，故甲胜的概率为11/16，乙胜的概率为5/16，因而甲和乙分别应得全部赌注的11/16和5/16。实际上，前四种情形表示只需掷两次就可分出胜负，往下的六种情形表示只需掷三次即可分出胜负。但如果这样表示，就不好用古典概率进行计算了。
计算古典概率，可以如上例用穷举法数清一个事件所含元素的个数，但借助于组合计算可以简化计算过程。上例中，“甲胜”这一事件所含元素个数为
。这种用组合数学方法计算只涉及有限个基本事件的概率问题，也称组合概率。需要强调的是，这里应十分注意“等可能”这个条件，即每一个基本事件具有相同的概率。J. le.R.达朗贝尔在考虑掷两个硬币的试验中，曾错误地认为“出现一个正面朝上，一个反面朝上”的概率是 1／3。事实上，此试验有｛(+ +)，(+ -)，(- +)，(- - )｝四个等可能的基本事件， 而出现一正一反这一事件含(+ -)、(- +)两个基本事件，其概率应为1/2。对于由有限个基本事件构成的古典概率模型，可以把事件A的概率P(A)看成是在事件域F上定义的函数，它具有下列三个性质：①对任意的事件A，0≤P(A)≤1；②必然事件Ω的概率为1；③若A，B不相容，则 P(A∪B)=P(A)+P(B)。其中③称为可加性公式，它是计算概率的重要法则。例如有一批产品总数为1000，其中含10个废品，从中随机抽出20个，求这20个中有废品的概率。用A表示这一事件，如直接计算A的概率，就要依次计算20个中恰有1个、2个、直至10个废品的概率各为多少，再求和。但A的对立事件Ac是抽出的20个中不含废品的事件，而它的概率容易计算，为
，根据③，即得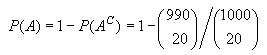
。几何概率 在建立古典概率的同时，人们就注意到只考虑取有限个元素构成的基本空间是不够的。把等可能思想发展到含无穷多个元素的基本空间，就产生了几何概率。其基本思想可以表达为：设Ω是平面上一个可求积的区域，域F由Ω中一切可求积的子集组成。设A∈F，μ(A)表示A的面积，随意扔一个点到Ω中，按照等可能性的思想，可认为点落入Ω内任何一部分的概率与这一部分面积成正比，而与这一部分的形状及其在Ω内的位置都无关，因此，落入A的概率P(A)=μ(A)/μ(Ω)。下述的布丰（曾译蒲丰）投针问题是一个应用几何概率的典型例子。
设平面上有一族平行线，每相邻两条之间的距离为2，取一枚长为1的针，随意地把它扔到平面上，求针与直线相交的概率。用 x表示针的中点到离它最近的一条平行线的距离，用θ表示针与平行线的夹角，如图2
之a。(x，θ)完全决定针所落的位置，针的所有可能的位置为0≤x≤1，0≤θ≤π，即图2之b所示的矩形里的每一个点，矩形的面积为π。针与直线相交的充分必要条件是
它对应于图2之b中带阴影的部分，其面积等于
。用A表示“针与直线相交”这一事件，则P(A)=1/π。由此，多次投针，计算它与直线相交的频率，可以求出π的近似值。虽然这样做既费时又不精确，但这一思想有可取之处，因为在有了快速电子计算机之后，可以用电子计算机模拟投针试验来计算π的近似值，这样就看出其优越性了。许多像求 π的近似值这样表面上看起来和概率毫不相干的问题，都可以用几何概率加以解决。概率的频率定义 随着人们遇到问题的复杂程度的增加，等可能性逐渐暴露出它的弱点，特别是对于同一事件，可以从不同的“等可能性”角度算出不同的概率，从而产生了种种悖论，著名的贝特朗悖论就是一个典型的例子。另一方面，随着经验的积累，人们逐渐认识到，在做大量重复试验时，随着试验次数的增加，一个事件出现的频率，总在一个固定数的附近摆动，显示出一定的稳定性。R.von米泽斯把这个固定数定义为该事件的概率，这就是概率的频率定义（见概率论）。
从应用角度看，频率定义可以克服等可能性观点不易解决的某些困难，但从理论上讲，这种定义方法是不够严谨的。概率论的进一步发展，要求人们从古典定义、几何定义、频率定义中吸取能反映规律性的本质性质，克服它们各自的局限性，抽象出一种合理的定义，它既把以前各种有实际意义的定义作为特殊包含在内，又能满足现代科学对它所提出的更高要求，这就是Α.Η.柯尔莫哥洛夫的概率公理化定义。
概率的公理化定义 设基本空间Ω是一个任意给定的非空集合，它的元素用ω 表示。依据不同的考察对象，ω 可以代表种种不同的基本事件，但这对概率论的逻辑发展而言是无关紧要的。事件的全体F是Ω的某些子集构成的集类，为了研究无穷多个事件的关系，除了如同前述域的定义中要求Ω∈F以及“若A∈F，则Ac∈F”之外，还要求把“F中任意两个事件的并仍属于F”这一条件，强化为如果任意可列多个事件A1，A2…，都属于F，则它们的并
也属于F。这样的域F称为σ域或σ代数，也称事件域。对于由无穷多个基本事件构成的基本空间，这种强化是具有本质上的重要性的。对给定的基本空间Ω和σ域F，概率的公理化定义如下：概率P是F上的实值函数，即对每一A∈F，有一实数P(A)与之对应，且满足下面三条公理。
① 非负性 对一切A∈F，P(A)≥0；
② 规范性 P(Ω)=1；
③ 可列可加性 若A1，A2，…∈F，且两两不相容，则
。以上三条公理是古典概率性质的发展，从它们容易推出 P(═)=0，P(A)≤1，P(Ac)=1-P(A)等基本性质。公理③是把可加性公式扩展到可列无穷的情形，它在概率论中起着根本的作用。这样的公理化模型是由三个基本要素组成的，记为(Ω，F，P)，称为概率空间，它是一般测度空间（见测度论）的特例；P也称为可测空间(Ω，F)上的概率测度。事件独立性 独立性是一个使概率论区别于测度论的特有概念。考虑“甲扔硬币，乙掷骰子”的试验，求事件“硬币出现正面，骰子出现5或6”的概率。若把事件“硬币出现正面”记作A，事件“骰子出现5或6”记作B，则所求的是事件A∩B的概率。整个试验的基本事件的总数为12，而且是等可能的。A所含基本事件的个数为6，B所含基本事件的个数为4，而A∩B所含基本事件的个数为2，这样P(A)=6/12=1/2，P(B)=1/3，P(A∩B)=1/6，于是有P(A∩B)=P(A)·P(B)。对于任意两事件A和B，如果它们各自发生的概率与它们同时发生的概率满足P(A∩B)=P(A)·P(B)，则称它们为独立的。结合上例，独立性的这一定义与直观是一致的，因为甲和乙作试验是单独进行而互不影响的。对于n(n≥2)个事件A1，A2，…，An，如果对所有可能的组合都有
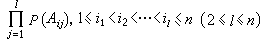则称这n个事件独立。这里，集合的有限交的记号∩常被省去， 如A
∩A
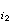，记为A
A
，A
∩…∩A
则简记为
，而以上的n-1组关系式必须都成立，缺一不可。下面的例子说明存在这样的三个事件A，B，C，它们是两两独立的，但整体上并不独立。考虑一正四面体，一面为红色，一面为蓝色，一面为黄色，剩下的一面为红蓝黄三色。以 A，B，C分别表示扔四面体时朝下的一面出现红、蓝、黄的事件，于是有P(A)＝P(B)＝P(C)＝1/2，且P(AB)=P(AC)=P(BC)=1/4，故A，B，C 两两独立，但是P(ABC)=1/4，P(A)P(B)P(C)=1/8，二者并不相等。
条件概率 独立事件同时发生的概率很容易从它们各自发生的概率算出，而为了计算不独立事件同时发生的概率就需要用到条件概率。设某城市有N个男人和M 个女人，其中患色盲者男性n人，女性m人。用Ω表示全体居民的集合，A表示全体女性居民的集合，B表示全体色盲患者的集合。某工厂要招聘一名化验员，要求不是色盲患者，问任意一位应聘的女性被厂方拒绝的概率是多大？这里所求的就是“女性中色盲患者”的概率，用记号P（B│A）表示。按等可能性原则，
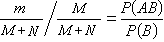，或P(AB)=P(A)P(B|A)。一般地，若P(A)>0，称P(AB)/P(A)为“已知A时，B的条件概率”，或“B关于A的条件概率”，记作P(B|A)。当A固定，B取遍F中的事件时，条件概率P(·│A)作为F上的函数，也具有公理化定义中概率的那些性质。如果对某个B，P(B│A)=P(B)，那么P(AB)=P(A)P(B|A)=P(A)P(B)，这表明A和B独立。关系式P(B│A)=P(B)可解释为不论有没有“已知A”的条件，B的概率不变，这是符合A和B独立的直观意义的。关于条件概率有三个重要公式：
①一般乘法公式设A1，A2，…An∈F，n≥2，P(A1A2…An-1)>0， 则
。② 全概率公式 设 A1， A2，…∈F，两两不相容，
，对一切 n 成立，则 P(A)＝
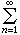
对一切A∈F成立。③ 贝叶斯公式 在②的条件下，对满足P(A)>0的A，有
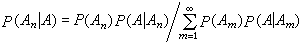。历史上有名的配对问题的解决是应用条件概率的典型例子。设有n个信封和n张信纸，分别编号为1至n，把信纸随意装进信封里，一个信封里恰好只装一张信纸，求“没有一个对号”这一事件的概率P0，以及对每一正整数r(r≤n)，求“恰有r个对号”的概率Pr。
用Ai表示事件“第 i号信纸恰装入第 i号信封”，则 P（Ai）=1/n。在 Ai发生的条件下，第 j 号信纸共有n-1个信封可供选择， 故 P（Aj｜Ai）=1/（n-1），因此 P（Ai Aj）= 1/n（n-1）， 其中 i≠j。类似地， 对1≤i1<i2<…ir≤n，
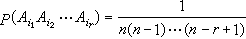，从而
。 根据逐步淘汰原则， 至少有一个对号的概率是
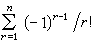，从而 
。再计算Pr，由于对指定的某r 张信纸，它们都对号的概率为
余下的 n-r张信纸没有一张对号的概率为
（即在P0中以n-r代替n），而r张信纸对号共有
种选法，故
以上只是就已知单个事件发生为条件定义的条件概率，这是简单情形的条件概率。由于人们对非独立性的认识逐步深入，用简单情形的条件概率不能满意地刻画深化了的非独立性，而需要就更一般的情形来定义条件概率。这一定义只是在有了测度论之后才能严格给出(见条件期望)。