积分学(卷名：数学)
integral calculus
与微分学联系密切，共同组成了分析学的一个基本分支──微积分学。积分学主要研究积分的性质、计算及其在自然科学与技术科学中的应用。积分学的最基本的概念是关于一元函数的定积分与不定积分。蕴含在定积分概念中的基本思想是通过有限逼近无限。因此极限方法就成为建立积分学严格理论的基本方法。定积分定义比较完整地概括了积分思想，也比较深刻地揭示了概念的实质。然而这样定义的积分，除非是在某些极为特殊的情况下，很难直接地用于实际的计算。通常的办法是先计算被积函数的不定积分，再利用牛顿-莱布尼茨公式算出它的定积分值。不过，即使是对于初等函数，计算不定积分的问题也不能完全地得到解决，因为初等函数的不定积分未必仍然是初等函数。所以不得不考虑进行积分的近似计算并且相应地引进一些非初等函数的新函数。所有这一切使得积分的计算成为很突出的问题。
定积分 促成定积分概念形成的一个问题是几何方面的计算平面上的曲边形面积。这个问题相当古老。尽管面积概念自古就已被直观地、经验地理解着，却缺乏一般可行的计算方法。如阿基米德等古希腊数学家，用所谓“穷竭法”算出了圆、弓形与抛物线弓形的面积。中国古代数学家刘徽创造了所谓“割圆术”，他从圆内接正六边形起算，令边数成倍地增加，再逐个算出正六边形，正十二边形，正二十四边形……的面积，然后用这一串面积序列来逼近圆面积。不过，古代关于计算面积的朴素思想远未达到形成面积概念的境界。他们只完成了一些特殊的曲边形面积的计算。直到17世纪，I.牛顿、G.W.莱布尼茨才明确地提出了面积计算的普遍方法。
曲边梯形的面积 是指[α， b]区间上的非负连续函数ƒ(x)与x轴及直线x=α和x=b围成的一块面积。由于曲线形总是用有限个这种图形组成的，因而计算它的面积是一个基本问题。首先可以把曲边梯形的面积S 划分成一些小曲边梯形的面积 ΔSi之和（图1
）：
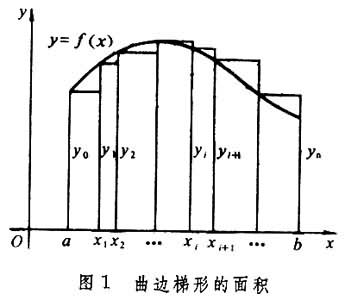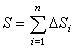，再用小矩形的面积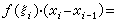
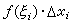来代替每一块小面积ΔSi。 和式
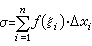表示各个小矩形面积之和，它与S的差别将随着小面积划分的细密程度的增高而愈来愈小。由于小面积的划分是通过对区间 [α， b]的划分来实现的，如果令λ为最大的区间长度，即
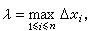那么曲边梯形面积就有极限表示：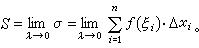
促使定积分概念产生的另一类问题是物理学方面的求变化过程中的积累量。例如，变速运动在一段时间[α，b]内行进的路程，变力使物体运动一段路程[α，b]所作的功等等。计算的方法仍然是将所求的量（路程l或功W）划分为“无穷小量”之和
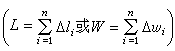，并用均匀变化过程的计算方法来近似计算 ΔЛi或Δwi。如果ΔЛi是时间间隔[ti-1， ti]中物体运动的路程，则可用在此时间间隔内的匀速运动所行进的路程υ(ξi)·(ti-ti-1)=υ(ξi)·Δti来近似地代替ΔЛi，其中 υ(ξi)可以是物体在 ti-1到ti之间任何时刻的速度。如果Δwi是变力F(s)在小段路程间隔[si-1，si]上所作的功，则可用在此小段路程上常力作功 F(ξi)·(si-si-1)＝F(ξi)·Δsi来近似代替Δwi，其中F(ξi)可以是物体在路程si-1 到si之间任何一点处所受的力。这时和式
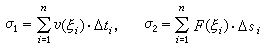与所求的量l、W 的差别，将随“无穷小量”划分的细密程度的增高而愈来愈小。由于所谓“无穷小量” ΔЛi或Δwi是通过对区间[α， b]的划分来实现的，若令λ为最大的小区间长度，那么所求的量是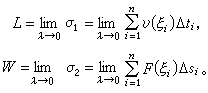
无论计算曲边梯形面积还是变速运动的路程或变力所作的功，都是对一个函数（ƒ(x)，υ(t)或F(s)）在一个确定的区间[α，b]上，求出其内在的一个确定的数值(S，l或W)，而且方法是共同的：都是在对区间[α，b]进行分划的基础上构造出一个特殊形式的和，然后求出其极限值。对一个抽象的定义在某个区间[α，b]上的函数 ƒ(x)，也可用同样的方法寻求它内在的某个确定的数值，而被称之为函数 ƒ(x)在区间[α，b]上的定积分。下面叙述的是诞生于19世纪的严格的定积分概念，它基于A.-L.柯西对连续函数的积分的研究以及（G.F.）B.黎曼关于某种不连续函数的积分的研究。
定积分的定义 设函数ƒ(x)定义在区间[α，b]上，在这区间上顺序插入任意若干分点：
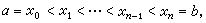从而把区间[α，b]分划为n个子区间，在每个子区间[xi-1，xi]上任取一点ξi并作和式
令λ表示分划的最大的子区间的长度。如果当λ→0时，和式σ趋于某一个确定的极限I，则称这极限I为函数ƒ(x)在区间[α，b]上的定积分或黎曼积分，记为
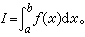这时又说函数ƒ(x)在区间[α，b]上是黎曼可积的。当[α，b]上的连续函数ƒ(x)≥0时，积分
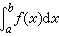有着明显的几何意义，它表示由曲线y=ƒ(x)及直线x=α，x=b，y=0所围成的曲边梯形的面积（图1）。至于一般的函数，如果规定x轴下面的曲边形的面积是负的，则积分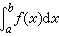给出了如图2中几部分“有向”面积的代数和。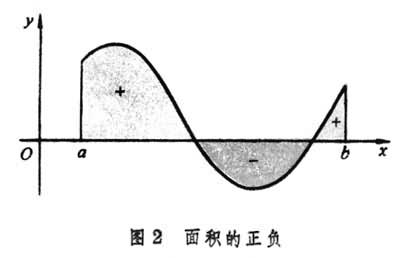
定积分的基本性质 定积分作为有限和的极限，仍保持着一些有限和所具有的特点。它对于积分区间是可加的，即
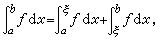而对于被积函数是线性的，即
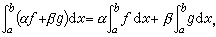式中α，β为常数；并且当ƒ ≤g 时，成立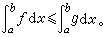
此外，还有分别关于被积函数与积分区间的中值定理：
第一中值定理 对于区间［α，b］上一个连续函数ƒ(x)与一个不变号的可积函数φ(x)，一定存在该区间上一点ξ，使得
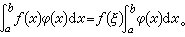
第二中值定理 对于区间［α，b］上一个单调函数ƒ(x)与一个可积函数g(x)，一定存在该区间上一点ξ，使得
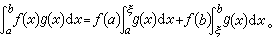
黎曼可积函数类 根据定积分的定义可以判断，凡无界函数都不是黎曼可积的。全体黎曼可积的有界函数组成的函数类称为黎曼可积函数类。区间[α，b]上的有界函数ƒ(x)黎曼可积的充分必要条件是
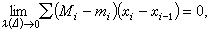式中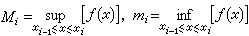 
分别是区间[xi-1，xi] 上ƒ(x)的上、下确界。这个充分必要条件刻画了黎曼可积函数类仅由那些不连续的范围不甚广的有界函数所组成。以上结论又可以确切地叙述为：黎曼积分存在的一个充分必要条件是被积函数在积分区间上有界，并且其不连续点能够被一些区间所覆盖，而这些区间的总长度可以任意小。定积分概念可以推广到广义积分、含参变量积分、多元函数在相应的高维区域上的积分(见多元微积分学)等。近代尤其重要的推广是对黎曼积分的定义加以改造而构成勒贝格积分的概念。勒贝格以他关于点集的测度概念为基础，建立的这一新的积分理论扩充了黎曼可积函数类，克服了黎曼积分在极限运算方面存在的局限性，使有关极限与积分交换次序的理论变得非常简明（见勒贝格积分）。
不定积分 某些实际问题的解决常常归结到寻求一个函数，使它以某一个已知函数为导数。例如，研究一个质点的非匀速直线运动，如果知道的是它在各个时刻的瞬时速度υ (t)，要想获得该质点所在的位置对时间的依赖关系，便归结到寻求一个函数s(t)，使它的导数恰等于υ(t)。一般地说，对于给定函数ƒ(x)， 求出一个或一族（如果运算结果不惟一）函数，使其导数为ƒ(x)的运算称为积分ƒ(x)。因此，如果积分ƒ(x)的结果是F(x)，则微分F(x)的结果便是ƒ(x)，所以积分是微分的逆运算。
原函数 如果函数F（x）的导数是函数ƒ（x），即
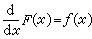，则称F(x)为ƒ(x)的一个原函数。ƒ(x)的原函数不是惟一的。例如F(x)加上任意常数后，其导数仍然是ƒ(x)。因此重要的事情是弄清楚，ƒ(x)的全体原函数有什么样的结构，或者说需要弄清楚ƒ(x)的任何两个原函数之间的关系。如果F(x)与G(x)都是ƒ(x)的原函数，对函数[F(x)-G(x)]在某一任意区间[x0，x]上应用微分中值定理可得F(x)-G(x)呏常数，这说明了一个函数的任意两个原函数之间至多只能相差一个常数。不定积分与原函数 函数 ƒ(x) 的不定积分指的是ƒ(x)的全体原函数，记为
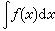。如果已知ƒ(x)的一个原函数F(x)，则有
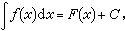式中C可以是任意常数。积分法 求函数的不定积分的一些基本法则。基于积分与微分的互逆关系，将微分公式倒转顺序，便立刻得到一些简单的积分公式：
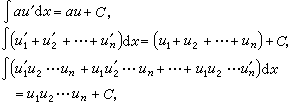
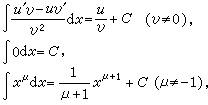
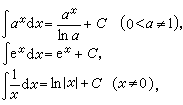
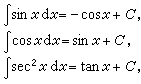
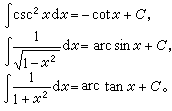相应于复合函数微分法的积分方法是换元积分法。若新旧变量间的关系是x=φ(t)， φ′(t)是连续函数，则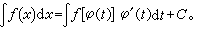
例如，令t=kx，则
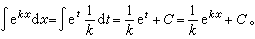令t=sinx，则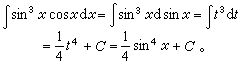
换元积分法扩大了积分公式的使用范围。
相应于乘积微分公式的积分方法是分部积分法：
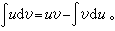
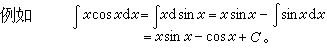
求不定积分比求导数要困难得多，即使一些简单的初等函数，它们的不定积分也不一定能用初等函数的有限形式表达出来。例如
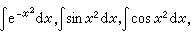
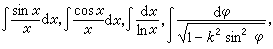
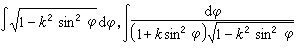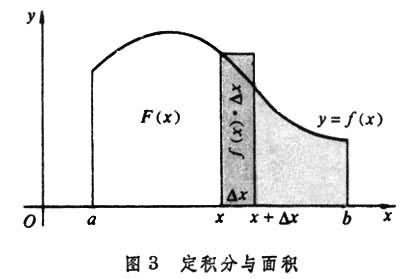
等都是“积不出来”的。但这些不定积分仍然可以用其他形式表明自身作为原函数的存在性。微分和积分的关系 以计算面积为背景的积分运算，从诞生的时候起，就显示了与微分运算的密切联系。牛顿和莱布尼茨首先在几何上发现了这个事实。如果ƒ(x)是区间[α，b]上的连续函数，由曲线y=ƒ(x)与x轴及α与x二点的纵坐标线围成的图形的面积（图3
）可以用积分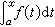
表示。它是x的函数，记作F(x)。当x有一个改变量 Δx，面积 F(x) 相应地有一个改变量ΔF(x)。几何上可以看出，表示ΔF(x)的主要部分的一小块矩形面积可以是 ƒ(x)·Δx 。对这一事实采用微分的符号来表示，就是
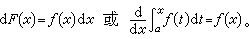在此基础上，得到了联系微分与积分的重要定理。微积分学基本定理 如果函数 ƒ（x）在区间［α ，b］上连续，则
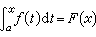在区间[α，b]内可微，而且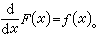
这就是说，对于任何一个连续函数ƒ（x）都有一个可以直接从定积分得到的原函数:
因此对于ƒ（x）的任意一个原函数G（x），也就总可以表示为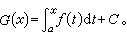
比较G(x)在x=α与x=b的不同形式，就得到了真正实现定积分计算的公式：牛顿－莱布尼茨公式
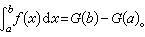这个公式说明在ƒ(x)的一个原函数可以求得的先决条件下（许多情况确实如此），定积分
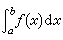的计算可以转化为求这个原函数G(x)在两点的函数值的差。这比直接使用定义去求和、取极限来计算定积分显然要容易得多。这个公式是微积分学基本定理的直接推论。微积分学基本定理的重要性就在于它把微分与积分从概念上和计算上同时联系起来，而成为微积分学形成的理论基础。定积分的计算 基于牛顿-莱布尼茨公式，通常应用的方法有换元法和分部积分法。
① 换元法
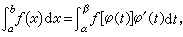这里要求的条件是:ƒ(x)在区间[α，b]上连续;φ(t)在区间[α，β]上连续并且适合φ(α)=α，φ(β)=b，α≤φ(t)≤b;φ ′(t)在区间[α，β]上处处存在并且可积。② 分部积分法
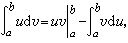这里要求的条件是函数u′，υ′在区间[α，b]上处处存在并且可积。定积分的近似计算 由于不少函数的原函数不是初等函数，有些即使是初等函数，其函数值也不一定容易计算，所以在实际计算这些函数的定积分时，往往要考虑通过被积函数来近似计算。近似计算方法的基本思想是：对被积函数进行适当的分划、求和，用有限和来代替积分的真值，并且同时给出这种代替的误差估计。普通的数值积分方法有：
① 矩形法
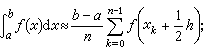其误差
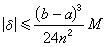，其中M是 |ƒ″(x)|在区间[α，b]上的最大值。② 梯形法
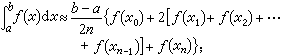其误差
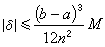，其中M是|ƒ″(x)|在区间[α，b]上的最大值。③ 抛物线法
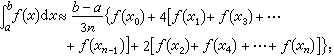其误差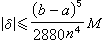
，其中M是|ƒ(4)(x)|在区间[α，b]上的最大值。上述近似公式称为辛普森公式。以上三个近似公式中的xk(k=0，1，…，n)是等分区间[α，b]的分点，
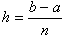称为步长，抛物线法中的n应是偶数。广义积分 黎曼积分只是在被积函数有界且积分区间为有穷的限制下定义的。但在应用中有时需要取消这些限制。这就导致广义积分概念的产生。广义积分包括无穷积分与瑕积分两种。
无穷积分 即积分区间为无穷的积分，被定义为正常的黎曼积分的极限：
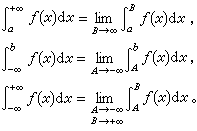这里的条件是ƒ(x)可积及所涉及的极限存在。这时也说相应的无穷积分是收敛的，否则就说是发散的。瑕积分 相应于函数ƒ(x)在区间[α，b]的某一端点或某一内点с 附近为无界的情形（该点便称为函数的瑕点），有
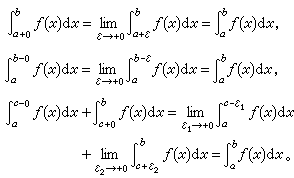这里条件也是ƒ(x)可积且所涉及的极限存在。这时也说相应的瑕积分是收敛的，否则就说是发散的。假如函数ƒ(x)在区间上有有限多个瑕点，则可以把这些瑕点当做分点，分别考察ƒ(x)在各个子区间上的瑕积分的收敛性，如果它们都是收敛的，就规定它们的和为原区间上的瑕积分。广义积分的收敛性定义与无穷级数的收敛性定义有许多相似之处。例如在无穷积分中，
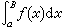的地位恰如无穷级数中的部分和
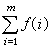一样。符号
也如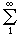
一样，即表示积分本身，在积分收敛时又表示积分值。在无穷积分与瑕积分中也有绝对收敛与条件收敛的概念以及相应的判别法，这些判别法在原则上也与无穷级数中的那些判别法一致（见级数）。柯西主值 柯西曾结合物理意义提出了积分主值的概念，它的定义是：
，
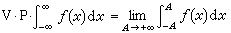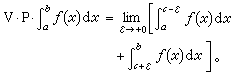在广义积分收敛时，积分值等于柯西主值。不过，在广义积分发散时，柯西主值却可能存在。例如：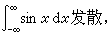
；
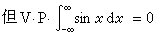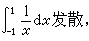
。含参变量积分 黎曼积分与广义积分的建立，可以提供一种确定并且研究函数的新方法。
假设ƒ(x，t)是一个定义在平面矩形区域R(α≤x≤b；α≤t≤β)上的二元连续函数，考虑它对x在区间[α，b]上的积分，在积分过程中被积函数所依赖的变量t始终保持某一个固定的值。这个积分称为含参变量 t的积分。由于积分值依赖于t而惟一确定，由此可以定义t的一个函数
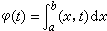。虽然在大多数情况下，这样确定的函数不是初等函数，但由于它具有定积分的特定形式，仍然可以用来研究这些函数的分析性质。例如，当函数ƒ(x，t)在R 上二元连续时，函数φ(t)在区间［α，β］上连续，并且
。当被积函数ƒ(x，t)关于参变量t的偏导数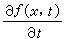
在R上存在并且连续时，则φ(t)在区间(α ，β)内可微，并且
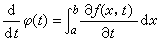。结合广义积分，可以建立函数含参变量广义积分。例如，具有无穷上限的含参变量广义积分
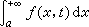，如果对t在其取值区间［α，β］上的一切参变量值，相应的积分都收敛，则可确定函数
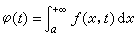。相应于函数项级数理论中“一致收敛”的重要概念，含参变量广义积分对参变量的一致收敛的概念也具有重要意义。如果对于任意的ε>0，存在Aε，当A≥Aε时，对于区间［α ，β］上的一切参量t，不等式
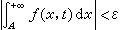都成立，这时就说含参变量广义积分
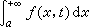在t的区间［α ，β］上一致收敛。使用一致收敛概念来研究函数φ(t)的分析性质，可得到与含参变量的黎曼积分相似的结论：当函数ƒ(x，t)在区域x≥α， α ≤t≤β上二元连续，积分
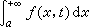在区间[α， β]上一致收敛时，函数
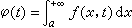在区间[α，β]上连续，并且
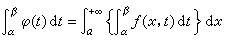。当ƒ(x，t)在区域x≥α，α ≤t≤β上二元连续并且具有连续偏导数
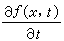， 同时积分 
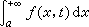在区间[α，β]上一致收敛时，函数φ(t)在这个区间上可微，并且
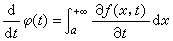。对于积分下限为－∞或积分上、下限都为无穷的含参变量的广义积分和被积函数无界的含参变量的瑕积分，也有类似的结论。
Γ函数
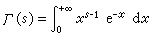是利用含参变量的广义积分确定一个非初等函数的重要例子。这积分当且仅当s>0时收敛；并且在区间α ≤s≤β上一致收敛，其中α与β为任意两个正数 (0<α<β)。 因此函数 Г(s)在任何s>0处都连续。Г函数的一个基本性质是Г(s+1)=s·Г(s)。根据这一性质可得到n!的表达式
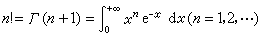。斯特林公式 上述表达式由于其中积分对于任何实数n>-1都有意义，可用来定义任何一个实数 n( >-1)的“阶乘”n!，并推导关于一个很大的数阶乘的近似估计
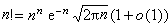。这个公式被称为斯特林公式。