函数构造论(卷名：数学)
constructive theory of functions
函数构造论中的主要研究课题，是由逼近论中正定理和逆定理两部分构成。所谓正定理就是从函数的结构性质（连续性、李普希茨条件、可微性等）来导出用n次多项式(或其他函数系)逼近函数时，其最佳逼近值（又称最佳逼近度）趋向于零的速度估计；所谓逆定理就是用n次多项式（或其他函数系）逼近函数时，从其最佳逼近值趋向于零的速度估计式来导出函数本身的结构性质。因此，研究函数的结构性质就可以化归为研究用多项式（或其他函数系）逼近时，其最佳逼近值趋向于零的速度。
设g(x)是以2π为周期的实轴上的连续函数，则用n次三角多项式逼近时的最佳逼近值E奱(g)定义为：
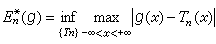。其中下确界是对于所有次数不超过n的三角多项式Tn(x)取的。设ƒ(x)是区间[α，b]上的连续函数，则用n次多项式逼近时的最佳逼近值En(ƒ)定义为：
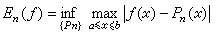，其中下确界是相对于所有次数不超过n的多项式Pn(x)取的。有关正定理的最早结果是由D.杰克森获得的。他得到
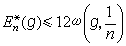，式中
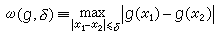称为g(x)的连续模。事实上，2n-2次三角多项式
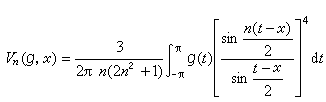称为杰克森算子，满足
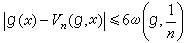。若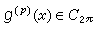
（p是自然数），则
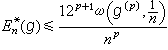。设ƒ(x)在[α，b]上有p阶连续导数，则对任意n>p，有
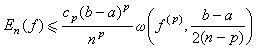，这里сp为只依赖于p的常数，且在定义连续模时要限制x1与x2都位于[α，b]上。此外，还可以用k 阶连续模
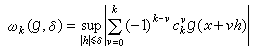来估计E奱(g)，相应地也可估计En(ƒ)。对于逆定理，最早的结果是由С.Η.伯恩斯坦获得的。对于g∈C2π，若对任意n，满足
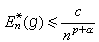（с为常数），式中p为非负整数，0＜α ≤1，则可推出
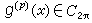，且
但是对于定义在区间[α，b]上的函数ƒ，由
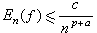只能推出上述结果在(α，b)中的任意闭区间上成立。这是因为在证明中用到多项式的微商可以被多项式本身最大值来进行估计的伯恩斯坦不等式，而这对于三角多项式Tn(x)与代数多项式Pn(x)是不同的，即 
，
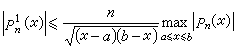。实际上，用代数多项式进行逼近时，其正定理应该依赖于点x的分布：在区间[α，b]的两个端点处，逼近的阶比内部要高。后来，Α.Ф.季曼得到改进的定理如下：
设ƒ
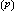(x)在[-1，1]上连续，则对任意n，存在n次多项式Pn(x)，使
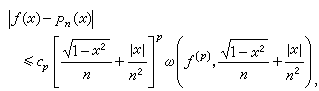式中сp是只依赖于p的常数。由此看出，在区间的两个端点处，逼近阶为
，而在区间内部逼近阶为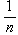
。至于逆定理，若对于任意的n，存在n次多项式Qn(x)，使得
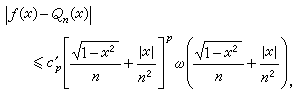式中с孡是只依赖于p的常数，ω(δ是某个连续函数的连续模，则可推出ƒ
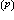(x)在[-1，1]上连续，且其连续模满足
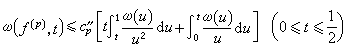，式中с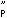
是只依赖于p的常数。此外，对于
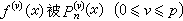逼近时也有类似的估计式。从复数域的观点来看，正定理中逼近的阶是依赖于区间[α，b]上点的外角；在[α，b]的两个端点，外角为2π，因此逼近阶为
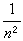，在(α，b)内的点，外角为π，因此逼近阶为
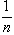。用这样的观点可以将实轴区间上的逼近推广到复平面区域上去，这时逼近的阶也依赖于点在区域边界上的分布，逼近的精度依赖于点在边界上外角的大小。