欧拉角(卷名：力学)
Eulerian angles
用来唯一地确定定点转动刚体位置的三个一组独立角参量，由章动角θ、进动角ψ和自转角嗞组成，为L.欧拉首先提出，故得名。它们有多种取法，下面是常见的一种。
如图所示，由定点O作出固定坐标系Oxyz 以及固连于刚体的坐标系Ox′y′z′。以轴Oz和Oz′为基本轴，其垂直面Oxy和Ox′y′为基本平面。由轴Oz量到Oz′的角度θ称为章动角。平面zOz′的垂线ON称为节线，它又是基本平面Ox′y′和Oxy的交线。在右手坐标系中，由ON的正端看，角θ应按逆时针方向计量。由固定轴Ox量到节线ON的角度ψ称为进动角；由节线ON量到动轴Ox′的角度嗞称为自转角。由轴Oz和Oz′正端看，角ψ和嗞也都按逆时针方向计量。欧拉角(ψ，θ，嗞)的名称来源于天文学。
三个欧拉角是不对称的，且在几个特殊位置上具有不确定性（当θ＝0时，嗞和ψ就分不开）。对不同的问题，宜取不同的轴作基本轴，并按不同的方式量取欧拉角。
若令Ox′y′z′的原始位置重合于Oxyz，经过相继绕Oz、ON和Oz′的三次转动Z(ψ)、N(θ)、Z′(嗞)后，刚体将转到图示的任意位置（见刚体定点转动）。变换关系可写为：
R(ψ，θ，嗞)=Z′(嗞)N(θ)Z(ψ)，式中R、Z′、N、Z是转动算子，并可用矩阵表示如下：
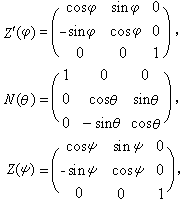
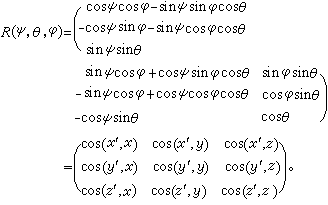在进行转动算子的乘法运算时，应从最右端做起。刚体上任一点Q在两个坐标系中的坐标x、y、z和x′、y′、z′都可以通过矢径
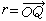的模和方向余弦来表出。两组坐标之间有如下变换关系：x＝x′cos(x，x′)+y′cos(x，y′)+z′cos(x，z′)，y＝x′cos(y，x′)+y′cos(y，y′)+z′cos(y，z′)，z＝x′cos(z，x′)+y′cos(z，y′)+z′cos(z，z′)。反变换只须在同名坐标间对调记号。
如果刚体绕通过定点O 的某一轴线以角速度ω转动，而ω在与刚体固连的活动坐标系Ox′y′z′上的投影为
、
、
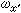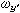，则它们可用欧拉角及其微商表示如下：
＝夗sinθsin嗞＋夝cos嗞，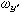
＝夗sinθcos嗞－夝sin嗞，
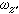＝夗cosθ＋夓。由上式可以看出，如果已知ψ、θ、嗞和时间的关系，则可用上式计算角速度ω在活动坐标轴上的三个分量；反之，如在任一瞬时已知t和ω的各个分量，也可利用上式求出ψ、θ、嗞和时间t的关系，因而也就决定了刚体运动。我们通常把上式叫做欧拉运动学方程。