配分函数(卷名：化学)
partition function
统计力学的基本概念之一，所有的热力学量都可由它求算。
单粒子配分函数 设单粒子的能级用εi(i＝1，2，3，…)表示，各个能级εi分别对应ωi个量子态（即εi的简并度为ωi）。ωiexp(-εi/kT)称为能级εi的有效量子态数，式中k为玻耳兹曼常数；T为热力学温度。另外，也可以对单粒子的量子态用1，2，3，…，r编号，第r个量子态的能量用εr表示，exp（-εr/kT）称为这一个量子态的有效量子态数。单粒子所有可及有效量子态数的总和称为单粒子配分函数q：
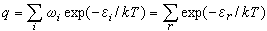式中
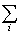是对可及能级求和；
是对可及量子态求和。一个粒子包括有平动、转动、振动等运动形态，如果这些运动形态彼此独立（或近似独立），则粒子配分函数可分解成各运动形态配分函数的乘积，称为配分函数分解定理。在化学反应中，一个体系变化前后核保持不变，除某些特殊情况外，核配分函数不予考虑，q便可表示成：
式中qt、qr、qv、qe分别为平动、转动、振动、电子配分函数。平动配分函数 一个质量为m的粒子，在体积V内自由运动时，粒子不受力，所以势能是常数。为简便起见，通常将势能作为零，实际上是将粒子的静止态作为平动能量的零点。根据量子力学，自由粒子的平动能级εt为：
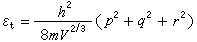式中h为普朗克常数，平动量子数p、q、r的取值为1，2，3，…。对应于上述能量零点的平动配分函数qt为：
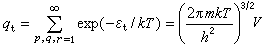平动配分函数是宏观参量温度、体积的函数，而且与体积成正比，因此，单位体积的平动配分函数只是温度的函数。转动配分函数 对于刚性异核双原子分子，设两原子绕通过质心且垂直于两核连线的轴的转动惯量为I，则分子绕质心转动的转动能级公式为：
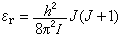式中J为转动量子数，取值为0，1，2，3，…。能级的简并度为：ωr＝2J+1转动配分函数为：
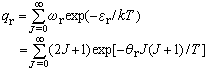式中θr为分子的转动特征温度。当Tθr时，上式求和可用积分代替，结果为：
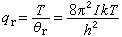实际上，所有直线分子的转动配分函数在Tθr时都可表示为：
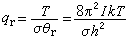非对称分子的σ＝1，对称分子的 σ＝2。σ称为分子的对称数，它来源于分子的一定对称性。对非直线性分子，一个分子在物理上所有相同取向的数目称为分子的对称数，σ等于分子绕各个独立的对称旋转轴转动时，容许分子取向相同的数目之和。设分子具有ni个独立的i重旋转轴，则求算分子对称数的公式为：
振动配分函数 一维谐振子以自然平衡位置为能量零点的能级公式为：
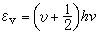式中v为频率。振动量子数v的取值为0，1，2，3，…。各能级都是非简并的，因而一维谐振子的配分函数为：
式中θv为振动特征温度。电子配分函数 原子或分子中的电子也有它的能级和量子态。设电子能级与其简并度分别用εei、ωei(i＝0，1，2，…)表示，如果选电子最低能级为能量零点，即取εe，0＝0，则电子配分函数为：
