索末菲椭圆轨道理论(卷名:物理学)
Sommerfeld's elliptical orbit theory
A.索末菲在玻尔氢原子理论的圆轨道基础上发展了椭圆轨道理论,认为电子在核的库仑场中运动,其轨道一般应为椭圆。索末菲假定在极坐标系中电子的允许轨道必须满足两个量子条件
 式中n嗞和nr都是正整数,分别称为角量子数和径量子数。核库仑吸引力是一种有心力,故电子的角动量p嗞在周期运动中为恒量
式中n嗞和nr都是正整数,分别称为角量子数和径量子数。核库仑吸引力是一种有心力,故电子的角动量p嗞在周期运动中为恒量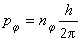 。利用这一关系,再用经典力学中粒子作椭圆轨道运动时总能量关系,算得氢原子中电子在椭圆轨道上的总能量为
。利用这一关系,再用经典力学中粒子作椭圆轨道运动时总能量关系,算得氢原子中电子在椭圆轨道上的总能量为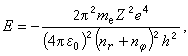 式中me是电子的质量,Z是原子核电荷数,e是电子的电荷量,ε0是真空介电常数, h是普朗克常数。如果令n=nr+n嗞,则电子在椭圆轨道上的能量与相应的玻尔轨道上的能量相同。整数 n称为主量子数。并且算得椭圆轨道的半长轴a为
式中me是电子的质量,Z是原子核电荷数,e是电子的电荷量,ε0是真空介电常数, h是普朗克常数。如果令n=nr+n嗞,则电子在椭圆轨道上的能量与相应的玻尔轨道上的能量相同。整数 n称为主量子数。并且算得椭圆轨道的半长轴a为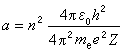 。半长轴a和半短轴b的关系为
。半长轴a和半短轴b的关系为 。对每一个半长轴,都有n个不同半短轴的轨道,按开普勒定律,作椭圆轨道运动粒子的能量只和长轴有关,故这些轨道上的电子具有相同的能量
。对每一个半长轴,都有n个不同半短轴的轨道,按开普勒定律,作椭圆轨道运动粒子的能量只和长轴有关,故这些轨道上的电子具有相同的能量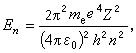 En只与n有关,与n嗞无关。
En只与n有关,与n嗞无关。考虑到电子质量的相对论效应,在偏心率不同的轨道上的影响是不同的,索末菲详细推导了相对论效应中电子能量,得到
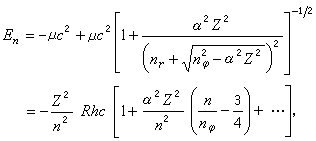 式中μ为电子与核的静折合质量,R为该原子的里德伯常数,с为真空中光速,
式中μ为电子与核的静折合质量,R为该原子的里德伯常数,с为真空中光速,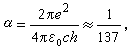 称为精细结构常数。可见,相对论效应使得主量子数n相同,但角量子数n嗞不同的椭圆轨道具有不同的能量,即同一个n值所标示的能级将分裂为n个相近的能级。据此也能解释光谱的精细结构。
称为精细结构常数。可见,相对论效应使得主量子数n相同,但角量子数n嗞不同的椭圆轨道具有不同的能量,即同一个n值所标示的能级将分裂为n个相近的能级。据此也能解释光谱的精细结构。1926年L.H.托马斯首先根据G.E.乌伦贝克电子自旋的假设,考虑到自旋轨道相互作用和相对论坐标变换效应,成功地解释了氢原子光谱精细结构谱线分裂。1927年P.A.M.狄喇克的相对论量子力学理论直接得到了相似的结果
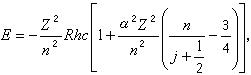 式中j取值
式中j取值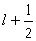 和
和 ,称总角动量量子数。狄喇克理论不仅能较好地定量解释氢原子光谱的精细结构,而且可直接导出电子的自旋磁矩。
,称总角动量量子数。狄喇克理论不仅能较好地定量解释氢原子光谱的精细结构,而且可直接导出电子的自旋磁矩。参考书目
褚圣麟编:《原子物理学》,人民教育出版社,北京,1979。
芶清泉编:《普通物理学(原子物理部分)》,人民教育出版社,北京,1965。