结构可靠度分析(卷名：水利)
analysis of structure reliability
结构在规定的时间内、规定的条件下具备预定功能的概率分析。如果预定功能仅指结构的承载能力，则这种分析称结构安全度分析。结构可靠度分析的数学基础是概率论及数理统计学。结构可靠度分析的目的，可以是对结构按给定的可靠度指标设计结构，也可以是对已建成结构进行可靠度校核。
一般过程 进行结构可靠度分析一般分三个步骤。
①收集与结构可靠度有关的随机变量(如风荷载、波浪荷载、地震荷载等)的试验、观测资料，进行统计分析，得出各随机变量的统计量（均值、标准差和分布类型）。
②计算结构的荷载效应，确定抗力，建立极限状态方程。荷载效应 S可以是结构的应力、应变、内力、位移等，它们可用力学分析方法求得。结构抗力 R是结构抗御破坏或变形的能力，如材料的屈服极限、构件截面的承载能力、容许的位移或变形等。S和R都是随机变量。它们的均值和标准差分别为┢S、┢R和σS、σR。设功能函数Z＝R-S。当Z
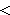0，表示结构失效；Z
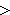0，表示结构可靠；Z＝0，表示结构处于极限状态。此式称为极限状态方程。③根据随机变量的统计量和极限状态方程可以计算；Z
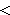0的失效概率Pf;Z≥0的可靠概率PS，即可靠度。Pf和PS两者是互补的，即Pf+PS=1。工程上采用可靠指标β作为设计的依据。对于S、R都是正态分布的情况有：
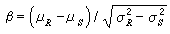β与Pf有一一对应的关系。Pf=Ф (-β )，Ф (-β )为-β 的标准化正态分布函数。在设计规范中，一般规定了适用于各种条件下的目标可靠指标值。分析方法 结构可靠度分析方法主要有三种。
①一次二阶矩法：采用随机变量的均值和方差作统计参数，并对极限状态方程在某点用泰勒级数展开近似地取一次项，来求结构可靠度。此法只适用于各个随机变量都是正态分布或对数正态分布的情况。
②JC法：即结构安全度联合委员会提出的近似方法，可用于随机变量为任意分布情况下的可靠度分析，其基本点是通过当量正态化处理，用正态分布来代替原来的任意分布，然后再用一次二阶矩法求解可靠度。此法在国际上应用较为广泛。
③蒙特卡罗法：又称统计试验法或概率模拟法，属渐近法。此法通过对随机变量进行随机抽样，代入功能函数式中考察结构是否失效，从而求得结构的失效概率和可靠度。此法需进行大量随机取样，计算工作量很大，需要编制程序在电子计算机上计算。
应用与发展 结构可靠度分析方法已在房屋、铁道、公路、水利等工程结构的设计规范编制中广为应用。一些重要的水工结构，如重力坝、拱坝和高桩码头等结构的安全度也采用了可靠度方法进行设计或校核。
结构可靠度分析正朝着结构动力可靠度、结构疲劳可靠度、结构断裂可靠度、结构体系可靠度、基于可靠度的结构优化设计，以及考虑模糊因素的广义可靠度等方向发展。
参考书目
赵国藩等编著：《工程结构可靠度》，水利电力出版社，北京，1984。
A.H-S.Ang and W. H. Tang， Probability Concepts in Engineering Planning and Design， Vol.1，2，John Wiley & Sons，New York，1975，1984.