雅可比行列式(卷名：数学)
Jacobian determinant
通常称为雅可比式(Jacobian)。它是以n个n元函数
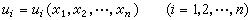(1)的偏导数
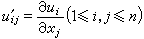为元素的行列式
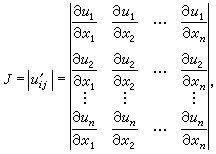常记为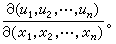
事实上，在(1)中函数都连续可微（即偏导数都连续）的前提之下，J就是函数组(1)的微分形式
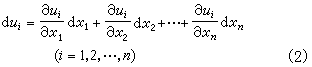的系数矩阵（即雅可比矩阵）的行列式。若因变量u1，u2，…，un对自变量x1，x2，…，xn连续可微，而自变量x1，x2，…，xn对新变量r1，r2，…，rn连续可微，则因变量(u1，u2，…，un)也对新变量(r1，r2，…，rn)连续可微，并且
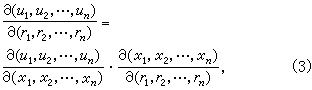这可用行列式的乘法法则和偏导数的连锁法则直接验证。而公式(3)也类似于导数的连锁法则。偏导数的连锁法则也有类似的公式；例如，当(u，v)对(x，y，z)连续可微，而(x，y，z)对(r，s，t)连续可微时，便有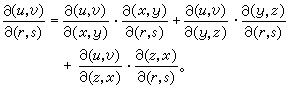
如果(3)中的r能回到u，
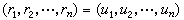，则(3)给出
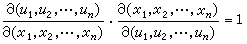。这时必须有
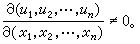(4)于是以此为系数行列式的联立线性方程组 (2)中能够把(dx1，dx2，…，dxn)解出来，作为(du1，du2，…，dun)的函数。而根据隐函数存在定理，在(u1，u2，…，un)对(x1，x2，…，xn)连续可微的前提下，只须条件(4)便足以保证(x1，x2，…，xn)也对(u1，u2，…，un)连续可微，因而(4)必然成立。这样，连续可微函数组(1)便在雅可比行列式不等于零的条件(4)之下，在每一对相应点u=(u1，u2，…，un)与x =(x1，x2，…，xn)的邻近范围内建立起点与点之间的一个一对一的对应关系。在n=2的情形，以Δx1，Δx2为邻边的矩形(ΔR)对应到(u1，u2)平面上的一个曲边四边形(ΔS)，其面积ΔS关于Δx1，Δx2的线性主要部分，即面积微分是
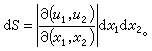这常用于重积分的计算中。如果在一个连通区域内雅可比行列式处处不为零，它就处处为正或者处处为负（其正负号标志着u-坐标系的旋转定向是否与x-坐标系的一致）。如果雅可比行列式恒等于零，则函数组(u1，u2，…，un)是函数相关的，其中至少有一个函数是其余函数的一个连续可微的函数。